「統計的に有意差がないため、2つのデータには差がない」──こんな結論の導き方は統計の誤用だとする声明が、科学者800人超の署名入りで英科学論文誌「Nature」に3月20日付で掲載された。調査した論文の約半数が「統計的有意性」を誤用しており、科学にとって深刻な損害をもたらしていると警鐘を鳴らす。
「統計的に有意差がない=違いがない」は間違い
例えば、ある薬の効能を調べたいとする。統計学では一般的に「仮説検定」を行って薬を与えたグループとそうでないグループを比較し、薬効の指標となる何らかのパラメータに統計的有意差があるかどうかを見る。仮説検定は、2つの事象の差異が偶然生じたものかどうかを統計的に結論付けるものだ。
もし、統計的有意差がある(薬を与えた群のパラメータの方が有意に大きい)なら「薬には効能がある」という結論を導けるが、有意差がなかった場合はどうだろうか。
「統計的有意差がある=薬効がある」なら「統計的有意差がない=薬効がない」と考えてしまいそうだが、声明ではこのように有意差がない場合、「“差がない”あるいは“関係がない”といった結論をしてはいけない」としている。
「ある」の反対は「あるとはいえない」
なぜなら、仮説検定では「帰無(きむ)仮説」と「対立仮説」という概念を用いるからだ。
帰無仮説はとりあえず立てた仮説(多くは検定者が否定したい仮説)であり、帰無仮説が間違っていると確信できる(棄却できる)ときに選ばれるのが対立仮説だ。
薬効の例での帰無仮説は「2群のパラメータは同じ」になる。これを検定手順を踏み棄却することで、「薬を与えた群のパラメータの方が対照群より大きい」という対立仮説を採択できる。
帰無仮説を棄却するかどうかの基準が有意水準だ。帰無仮説の基で計算したある検定統計量がその値となる確率(P値)が、有意水準(多くは5%)を下回れば、帰無仮説は棄却できる。つまり、「2群のパラメータは同じ」という仮説は誤りだと判断されるので、「薬を与えた群のパラメータの方が有意に大きい(薬効がある)」といえる。
問題はP値が有意水準より大きい場合だ。この場合、帰無仮説を棄却できないが、帰無仮説が正しいことも示していない。結果、「2群に有意差があるとはいえない」というあいまいな表現になる。
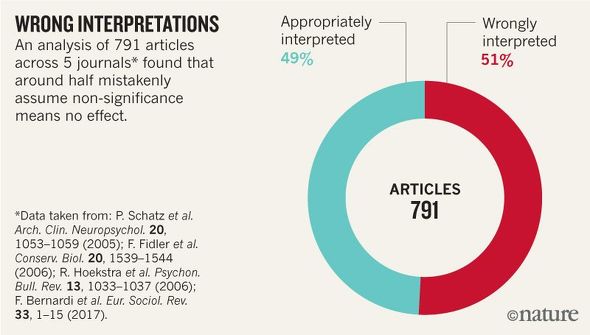
しかし、声明では「有意差がない=効果がない」と間違った推論をする論文も少なくないと指摘。実際に調べたところ、5つの論文誌・791文献のうち51%に誤りがみられたという。
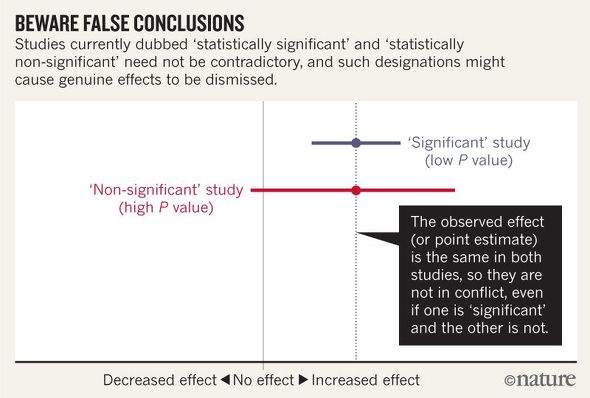
このような統計の誤用を続けると、実際にはデータの平均は同じなのに、異なる論文間で片方は効果があり(=有意差があり)、片方は効果がない(有意差がないことの誤解)という矛盾が発生してしまうこともあるとしている。
統計的有意性の代わりに信頼区間を
声明では「(あるないの二分法ではなく)統計の不確実性を受け入れる必要がある」とした上で、「(統計的有意差ではなく)信頼区間を使うべきだ」と指摘。さらに、「信頼区間」という単語も「互換区間」(compatibility intervals)に言い換え、計算結果への過剰な信頼を避けるようにすべきだとしている。
※信頼区間:区間推定において、ある確率(信頼係数)のもとで母数がその内に含まれると推定された区間のこと(統計WEBより)
「統計的有意性の誤用は、科学コミュニティーや科学的なアドバイスを頼る人たちに大きな損害を与えた。P値や信頼区間、その他統計的尺度はそれぞれ存在意義があるが、“統計的有意性”を使うのはもうやめるときだ」(声明)
Copyright © ITmedia, Inc. All Rights Reserved.
関連記事
 日本の科学研究「失速」 Nature記事、Webで全文公開中
日本の科学研究「失速」 Nature記事、Webで全文公開中
工学、分子生物学、コンピュータサイエンスなどの分野で論文出版数が減少していることなどを、取材やデータを基に解説している。- Nature誌、「Wikipediaの記事は取り下げない」
「Wikipediaとブリタニカ百科事典の精度は互角」という記事にBritannicaが反論したことを受け、Nature誌が記事の正統性を主張した。