“最も大きい素数”更新 「2^1億3627万9841-1」元NVIDIA社員が発見 文字に起こすと4000万字超え【訂正あり】

素数を探求するプロジェクト「GIMPS」は、今まで人類が見つけた数値の中で最も大きい素数「2^1億3627万9841-1」（1億3627万9841個の2を掛け合わせ、1を引いた値）を見つけたと発表した。

[松浦立樹，ITmedia]

　素数を探求するプロジェクト「GIMPS」は10月21日（現地時間）、今まで人類が見つけた数値の中で最も大きい素数「2^1億3627万9841-1」（1億3627万9841個の2を掛け合わせ、1を引いた値）を見つけたと発表した。これまで記録していた最大の素数よりも、1600万桁以上大きい値。十進数で表現した場合、桁数は4102万4320桁に及ぶという。

最も大きい素数を更新　値は「2^1億3627万9841-1」

　素数は、2以上の自然数の中で、1とその数自身以外に約数が無いもの（割り切れる数がないもの）を指す。中でも「2^n−1」（nは自然数）で表現できる素数のことを「メルセンヌ素数」と呼ぶ。これまでメルセンヌ素数は、51個存在していると知られており、その最大値は「2^8258万9933-1」だった。

　GIMPSは、このメルセンヌ素数を見つけるため1996年に発足したプロジェクトで、これまで18個のメルセンヌ素数を見つけてきた。

　今回、52番目のメルセンヌ素数を見つけたのは、米カリフォルニア州サンノゼ在住の研究者であるルーク・デュラントさん。デュラントさんは米NVIDIAの元社員で、23年10月ごろからGIMPSに参加。研究のため、多数のGPUサーバ上でGIMPSの解析ソフトウェア一式を実行、維持するためのインフラストラクチャを開発したという。

GIMPSの発表全文

　これにより1年間の検証を続ける中で、デュラントさんは新たな素数を発見。発見当時、デュラントさんが築いた「クラウドスーパーコンピュータ」ともいえる解析環境は、17カ国にまたがる24のデータセンター地域による数千台のGPUサーバで構成されていたという。第三者も検証を行ったところ、24年10月12日に新たな素数であることを正式に確認できたとしている。

　新たな素数を発見した功績として、デュラントさんには3000ドルの賞金が贈られるが、デュラントさんはこれを米アラバマ数学科学スクールに全額寄付する予定。

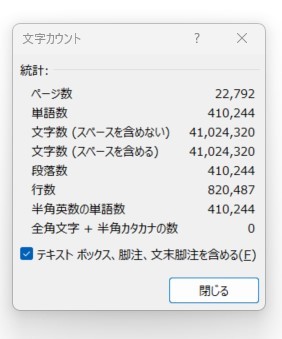
　なおGIMPSでは、今回見つかった素数を全桁書き起こししたテキストデータを無料配布中。テキストデータにもかかわらず、容量は18.3MBを記録。全文字をWordにペーストすると、改行も含むが全2万2792ページに及んだ。

全桁をWordにペーストした結果

【訂正：2024年10月22日午後8時】掲載当時、「2^136億27万9841-1」としていましたが、正しくは「2^1億3627万9841-1」でした。おわびして訂正いたします。