クラス図の落とし穴:UML BASIC LECTURE(1/3 ページ)
今回は、オブジェクト指向モデリングの際に利用されるUMLダイアグラムの中でも1番基本となるクラス図に関してポイントをまとめてみましょう。クラス図に関しても結構、誤解されている部分が見受けられるからです。
クラス図におけるクラスとは何か
まず、オブジェクト指向の基本を押さえておきましょう。オブジェクト指向の基本原理は、ひとことでいってしまえば、「クラス=概念=型=モジュール」という等式が成り立つことに尽きます。クラスが属性(インスタンス変数)と操作(メソッド)をカプセル化して定義する単位であり、かつモデル化対象に存在する概念を表現する際の単位であり、プログラミングの際に自由に導入できるユーザー定義可能なデータ型であり、それがオブジェクト指向でソフトウェアを作っていく際の基本的な管理対象としてのモジュールの単位になる、ということです。
この等式が成り立つとしたおかげでオブジェクト指向では、複雑な問題領域の構造や振る舞いを自由にモデリングしプログラミングにつなげていくことができるようになりました。モデリング上必要とあればいつでも新しいクラスを導入して概念を定義したり、設計や実装上必要とあれば自由にクラスを使って新たなデータ構造をユーザー定義し導入できるわけです。そして、ここが重要なポイントですが、うまくクラスを定義すればそれが概念としてもデータ型としても取り扱うことができる、すなわちソフトウェア上の管理対象としてトレース可能になる、というのがオブジェクト指向の偉大な発明なのです。クラスは概念でもありデータ型でもあるということがどれだけソフトウェア設計にとって柔軟性をもたらしているか考えてみてください。
ここで念のため用語の注意を一言。
オブジェクト指向では「クラスをデータ型とみなす」といった場合、そこで想定しているのは単純なデータ型ではなく、データ構造とそれに付随する操作(メソッド)のセットを合わせて(これがいわゆる「カプセル化」です)考えています。これは正確には「抽象データ型(abstract data type)」と呼ばれ、従来のデータ型の拡張概念です(図1)。
クラスは概念に対応する
特に分析モデリングでは、クラス図を用いて、その問題領域・業務世界の構造と仕組みをそこに登場する業務上の重要概念間の関係としてモデル化します。ですから、クラスを概念として扱う視点が非常に重要です。
モデル化対象である業務領域に登場する、その業務のしくみを表現するのに必要不可欠なキーとなる構成要素を概念クラスとして定義し、そうした概念クラスどうしの関係として業務を再構成したものが、業務の概念モデルです。
その概念クラスを特徴付ける性質(プロパティ)がそのクラスの属性として表現されます。またその概念クラスの業務領域における役割や責務(リスポンシビリティ)を明示的に定義したものがそのクラスの操作として表現されます(図2)。
ここでクラスを概念として理解する際の注意をひとこと。クラスは概念には対応しても集合には必ずしも対応しないので注意が必要です。通常、数学や論理学で使われる概念には内包的定義と外延的集合の両方が対応します。内包的定義とは、その概念の満たすべき条件を命題(真偽の定まる文)のセットとして表わしたものです。
つまり、文を用いてその概念の意味を定義するわけです。それに対し外延的集合とは、その概念で指示される具体的な実例すべてのことです。こちらは、意味は考えずにあくまでもそこに含まれる具体的なオブジェクトの集合によって実体的に概念を指定しようというものです。
実はオブジェクト指向では、クラスを用いて対応する概念の内包的定義を表わします。原理的には同様にその概念に対応する外延的集合を想定することができますが、クラスそのものはそこに定義してある属性のセットと操作のセットを満たすオブジェクトを生成しなさい、という宣言に過ぎません。したがって、クラス定義自体は対応する外延的集合と同一視することはできません(図3)。
では、オブジェクト指向で外延的集合を表わすにはどうするかというと、明示的にコレクションオブジェクトを用意し、そこにそのクラスのインスタンスの集合をプールすることになります。あくまでもコレクションオブジェクトがクラスとは別個に存在しなければならない点に注意してください。
集合の委員会パラドクス(コラム)
内包的な意味の定義と、実体の参照範囲にもとづく外延的な集合の指定との間の微妙な意味のずれを明らかにする面白い例があります。委員会のパラドクスと呼ばれるのがそれです。会員の中から委員を選んで委員会を構成します。それぞれ目的の異なる予算委員会と国際会議実行委員会の2つの委員会を定義したとします。ところが選んでみるとどちらの委員会もたまたま同じ4人の委員から構成されてることがわかりました。さて、予算委員会と国際会議実行委員会は同じ委員会と考えるべきなのか、それとも異なる2つの委員会と考えるべきなのか、というのがパラドクスの内容です。
同じ委員会だと考えるのが外延的な集合にもとづく理解です。異なる2つの委員会だと考えるのが内包的な意味の定義にもとづく理解です。そして、通常私たちは、内包的な意味役割によって対象を区別しますので、予算委員会と国際会議実行委員会とは異なる2つの委員会であり、たまたま構成要素が同じになっただけだと考えるはずです。このことから、日常的な認識世界では、概念は集合によって理解されているわけではないことがわかります。この事実は、実はオブジェクト指向モデリングではちゃんと区別してモデル化できます。図4のように同じ4人のメンバーを持つ2つの異なるコンテナSet[人]のインスタンスオブジェクトを導入すればよいからです。
ちなみに、数学的な概念はいちおう理論上は集合として外延的に構成・定義されていることになっています。したがって、数学上の概念としては、予算委員会と国際会議実行委員会とは同じ対象と見なされます。
Copyright © ITmedia, Inc. All Rights Reserved.
アイティメディアからのお知らせ
人気記事ランキング
- 初期侵入口は“またVPN” 日本医大武蔵小杉病院にランサムウェア攻撃
- 「2027年1月12日」は運命の日? サポート切れOSを使い続ける会社の末路
- ホワイトハッカーが明かす「ランサムウェア対策が破られる理由」と本当に効く防御
- SOMPOグループCEOをAIで再現 本人とのガチンコ対談で見えた「人間の役割」
- 富士通、ソブリンAIサーバを国内製造開始 自社開発プロセッサー搭載版も
- Googleが「AI Threat Tracker」レポートを公開 Geminiを標的にした攻撃を確認
- シャドーAIエージェントを検出 Oktaが新機能「Agent Discovery」を発表
- AIエージェント普及はリスクの転換点 OpenClawを例に防御ポイントを解説
- NTTデータ、仮想化基盤「Prossione Virtualization 2.0」発表 日立との協業の狙いは
- Apple、「macOS」や「iOS」に影響するゼロデイ脆弱性を修正 悪用確認済み
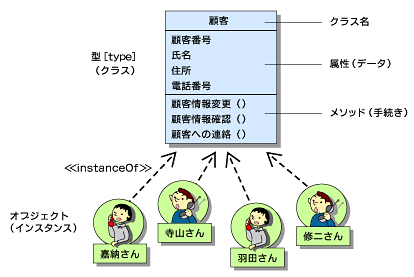 図1 データ型としてのクラス定義
図1 データ型としてのクラス定義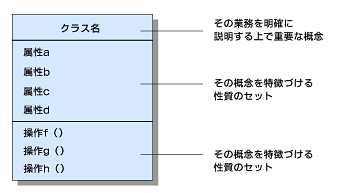 図2 クラス定義の構造とその概念的説明(上の文章の図化)
図2 クラス定義の構造とその概念的説明(上の文章の図化)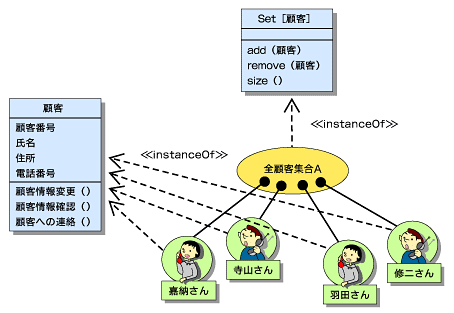 図3 クラスが指す概念とそれに対応するオブジェクトの集合
図3 クラスが指す概念とそれに対応するオブジェクトの集合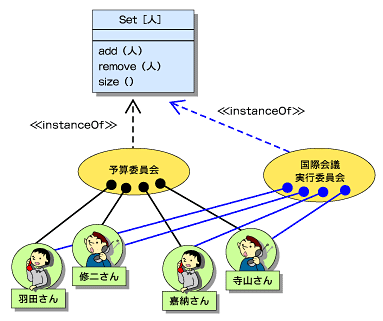 図4 同じメンバーからなる2つの委員会?
図4 同じメンバーからなる2つの委員会?