トップクラスだけが知る「このアルゴリズムがすごい」――「探索」基礎最速マスター：最強最速アルゴリズマー養成講座（3/4 ページ）

[高橋直大，ITmedia]

今回の問題

　今回の問題は、SRM456 Div1Medium／Div2Hardからの出題です。最近TopCoderに登録して出場したことのある方は、解いたばかりかもしれません。

John has some sticks of various lengths. You are given a int[] sticks, where each element is the length of a single stick.

He is allowed to perform at most C cuts. With each cut, he chooses one of his sticks and divides it into exactly two sticks of arbitrary positive lengths （the sum of their lengths must equal the length of the original stick）. Each of these sticks can then be chosen again when making subsequent cuts.

After he performs all his cuts, he sorts the sticks in non-increasing order by length and chooses the K-th （1-based） stick. Return the maximal possible length of the stick he chooses. Note that he must perform at least as many cuts as are required to end up with K or more sticks.

Constraints

- sticks will contain between 1 and 50 elements, inclusive.

- Each element of sticks will be between 1 and 1,000,000,000, inclusive.

- C will be between 1 and 1,000,000,000, inclusive.

- K will be between 1 and n + C, inclusive, where n is the number of elements in sticks.

　問題を簡単に日本語に訳すと、このようになります。

最初に、50本までの、長さが自然数である棒が与えられます。これらの棒は、C回まで好きな位置で切断して2つに分けることが可能です。ここで、K番目に長い棒の長さを最大にしたいとき、その長さは幾つになるでしょうか？

　これだけでは直感的に分かりづらいので、例を考えてみましょう。

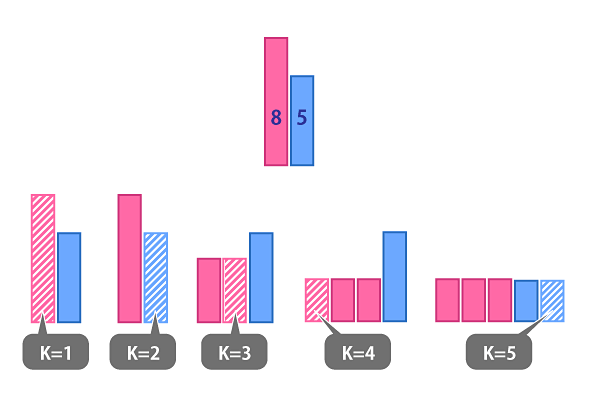
　長さ8と5の棒があり、Cが3、つまり全部で3回まで切ることができる、としましょう。ここで、K=1のとき、つまり1番長い棒の長さを最大にしたいときは、当然棒を切る必要はなく、答えは8となりますね。

　では、K=2のとき、つまり、2番目に長い棒の長さを最大にしたいときは、どうすればよいでしょうか？　これも、棒を切る必要はなく、答えは5となります。もし棒を切ったとしても、長さ8の棒で、長さが5以上の棒を2本作ることはできません。

　では、K=3、つまり、3番目に長い棒の長さを最大にしたいときは、どうすればよいでしょうか？　そもそも、最初に棒が2本しかないので、少なくとも1回切って、長い棒を作らなければなりません。この場合の最善手は、長さ8の棒を真ん中で切ることで、こうすると、長さ4の棒を2つ作ることになります。これを、K=5まで考えていくと、下の図のようになります。

　ちなみに、今回の問題では、最初にある棒の数は50本以下、長さは10億以下の整数、Cは10億以下、Kは棒が作成可能な範囲、となっています。切ることのできる回数が非常に多いところが、今回の問題で悩ましいところです。

　今回の問題についても、取り組みやすいように、問題挑戦用のソースコードを用意しました。問題側で設定されたサンプルデータが前半に5つと、本当に正しいかどうかを検証するための凶悪なデータが後半に5つあり、それぞれ自動でチェック可能になっていますから、気軽に挑戦することが可能になっています。C++、C#、Javaの3種類を用意しましたので、好きな言語で挑戦してみましょう！

ソースコードのダウンロードはこちらから

今日の問題のヒント

　今回の問題も、慣れないうちは非常にとっつきにくいタイプの問題です。この連載をお読みいただいている方の中にも問題を見て挑戦意欲がそがれてしまった方もおられるかもしれません。

　しかし、実はこの問題、TopCoderDiv1での最速提出時間は3分台と、慣れればEasy問題並みの速度で解くことのできるものだったりします。

　この問題は、数学的に美しく解いたりできるものではないと思いますので、普通は探索を使って解くことになります。ここで、切る回数が10億回までということがネックになります。例えば、「それぞれの棒ごとに切る回数を振り分ける」という方法では、最大50本の棒に10億回の切る回数を振り分けなければならず、さらに切る場所が自由になっていますので、途方のない計算量になってしまいます。ここをどのように工夫するかが今回の鍵になります。

　ここで大切になるのが、「問題を別の角度から見る」ことです。ほんの少しの言い換えをすることで、問題が一気に簡単なものに変わってしまいます。はじめのうちは難しいと思いますが、じっくり考えて解いてみましょう。そうしたポイントに気づくようになれば、解決できる問題が一気に増えるはずです。

　さて、それでは、次のページから、解答に移ります。