トップクラスだけが知る「このアルゴリズムがすごい」――「探索」基礎最速マスター:最強最速アルゴリズマー養成講座(1/4 ページ)
プログラミングにおける重要な概念である「探索」を最速でマスターするために、今回は少し応用となる探索手法などを紹介しながら、その実践力を育成します。問題をグラフとして表現し、効率よく探索する方法をぜひ日常に生かしてみましょう。
まだまだ活用可能な探索
前回の「知れば天国、知らねば地獄――『探索』虎の巻」で、「探索」という概念の基礎について紹介しました。すでに探索についてよく理解している方には物足りなかったかと思いますが、「問題をグラフとしてうまく表現し、そのグラフを効率よく探索する」というアルゴリズマー的な思考法がまだ身についていなかった方には、得るものもあったのではないでしょうか。
前回は、「幅優先探索」と「深さ優先探索」という、比較的単純なものを紹介しましたが、今回は、少し応用となる探索手法から紹介します。現状でも少し数学よりの連載になっていますが、「あえて」さらに数学的な例を挙げてみます。
分かる、二分探索
まずは、以下の問題をご覧ください。
x≧0とするとき、x^3+x^2+x=1となるxの値を求めよ
さて、皆さんならこの問題をどのように解くでしょうか。数学的には因数分解や3次方程式の解の公式を用いて解くことになるのでしょうが、筆者はあまりそのような素直な解法で解こうとは思いません。ここで探索が登場します。
まずf(x)=x^3+x^2+xとおきます。ここで、f(x)が1より大きくなる例と小さくなる例を考えて、f(0)=0、f(1)=3の2つを見つけます。ここで、x≧0においてf(x)は明らかに単調増加な関数ですので、求める答えは0から1の間にあることが分かります。
では、間を取ってx=0.5のときはどうでしょうか? f(0.5)=0.875ですので、これは1よりも小さい値となり、求める答えは0.5より大きいことが分かります。つまり、求める答えの範囲は0.5から1の間にあるということになります。少しずつ範囲が狭まってきましたね。これを繰り返していくとどうなるでしょうか?
上図のように、この工程を繰り返すだけで、簡単に答えを求めることができます。「ちょっと待て、この方法だと正確な値が求まらないのではないか?」と思われるかもしれませんが、コンピューターの小数の精度の問題がありますので、1回の工程で誤差が半分になることを考えれば、十分に繰り返すと誤差をほぼ0にすることは容易に可能なのです。
このようなアルゴリズムのことを、「二分探索」と呼びます。前回紹介した探索のイメージとは大幅に異なっているな、と思われた方もおられるかもしれません。しかし、よく考えてみれば、実は前回説明していた探索と考え方はほとんど変わらないのです。
今回のケースでは、最初の頂点が「0≦x≦1」となります。この下に「0≦x≦0.5」と「0.5<x<1」の2つの頂点に枝分かれします。もちろん、この2つのうち、条件を満たすのは片方だけしかないので、片方は「枝刈り」が行われ、それ以上の探索はされなくなります。このように、即枝刈りが行われてしまっているので、結果的に一本道になってはいますが、前回まで説明していた探索とほとんど同じものなのだといえるのです。
探索の基本が理解できていれば、ほかにもいろいろと工夫の仕方はあるでしょうし、いくらでも応用が効きます。今回は、数学的に求めることができる関数を用いましたが、単調増加、または単調減少するようなものに対してなら何にでも使えます。
また、今回は真ん中で切って2つに分けましたが、少し工夫して3つに分けることで、上に凸であったり、下に凸であったりする関数の最大値や最小値を求めることもできます。これを「三分探索」と呼び、これに黄金比を用いてさらに高速化を行った「黄金探索」なども存在します。ここでは詳細まで述べませんが、これらも探索です。興味のある方は、一度自分でどのようなものかを考えてから、調べてみてください。
探索マスターになるには
さて、ここまで、探索について例を挙げながら紹介してきました。しかし、まだピンと来ていない方がいるかもしれませんので、ここで探索をおおざっぱに定義しておきます。
探索とはつまり、
コンピューターのマシンパワーを生かして力ずくで問題を解いてしまおう!
ということであると筆者は考えます。
探索を用いると、きれいな解法よりは少し時間がかかってしまいますが、それぞれの問題に対して必ずしもきれいな解法が存在するとは限りませんし、きれいな解法というのは、少し問題が変わると対応できなくなってしまうものです。
その点において、探索は強力です。探索は一見力技ですが、一言で探索といっても、工夫の仕方はこれまで見てきたように複数ありますし、「どのように探索するのか」ということを常に頭に置いておかなければ、探索を使いこなすことはできません。ある探索のルールではうまく行かなかったとしても、問題を別の角度から見つめ、別のルールで探索が使えないかを考えてみる、ということを常に意識するのが、探索マスターへの第一歩なのです。
とはいえ、すでに皆さんは探索の基礎ができつつあります。次ページでは実際どのようにグラフを構築して、どのように探索をすればよいかをイメージする実践的な機会を用意しました。自身の理解度を確かめる意味でも、また、それが案外難しい(と思えた)問題でも通用することを体感してもらいたいと思います。
Copyright © ITmedia, Inc. All Rights Reserved.
アイティメディアからのお知らせ
人気記事ランキング
- 知らない番号でも一瞬で正体判明? 警察庁推奨アプリの実力を検証
- AD DSにSYSTEM権限取得の脆弱性 Microsoftが修正プログラムを配布
- .NETにサービス停止の脆弱性 広範なアプリケーションに影響
- Microsoft 365の新プラン「E7」は“AI盛り盛り”で99ドル E5にはない魅力は?
- ZIPファイルの“ちょっとした細工”で検知停止 EDRも見逃す可能性
- M365版「Cowork」登場 Anthropicとの連携が生んだ「新しい仕事の進め方」
- ★4を目指すのは正解か? SCS評価制度が企業に突き付ける“本当の論点”
- 本職プログラマーから見た素人のバイブコーディングのリアル AIビジネス活用の現在地
- 偽のTeamsサポートで新型バックドアを設置 巧妙な手口に要注意
- データ激増時代に変化するIT部門の役割 データガバナンス実装の現実解
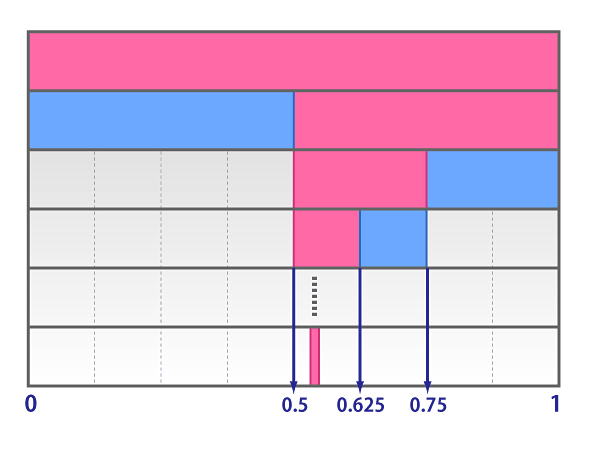 求める答えの範囲はどんどん狭まっていきます
求める答えの範囲はどんどん狭まっていきます