平均にもいろいろある あなたが本当に求めたいのは?:算術に加重……(1/3 ページ)
自然科学でも社会科学でも、データをあれこれと分析して、そこから仮説や命題を裏付けたり否定したりするような結果を導く。こうしたデータの分析のうち、頻繁に行われるのが、「平均をとる」という作業である。
通常、平均は、データを抽出した元の集団の傾向を表すものと考えられている。このため、確率論や統計学では、平均に関する定理が多く、その考察が欠かせないものとなる。
平均は、小学校の算数で割り算をマスターした後に、高学年くらいから身に付けるものだ。各データの値を足し算した結果を、データの個数で割り算して、平均が計算される。例えば、ある学校のクラスで生徒の平均身長を求めるには、各生徒の身長の合計を生徒の人数で割ればよい。これは「算術平均」と呼ばれる。最も単純で、分かりやすい平均である。
しかし、算術平均が役に立たない場合もある。
例えば、ある高級青果物店では、リンゴを1個400円、ミカンを1個100円で売っているとする。ある日、この店でリンゴが200個、ミカンが600個売れた。リンゴとミカンを合わせた平均単価はいくらだろうか。
この場合、2つの単価の算術平均である250円〈=(400+100)÷2〉には意味がない。平均単価を求めるには、合計の売上高を、合計の売上個数で割り算する必要がある。売上高は、リンゴ8万円、ミカン6万円で、合計14万円。これを合計の売上個数800個で割り算した、175円が平均単価となる。これは「加重平均」と呼ばれる。
また、成長率や伸び率など、物事の変化を表す率の平均には、別のものが必要になる。預金の利率で考えてみよう。
預金の利率は、複利で表すと扱いやすい。これは、最初に預けた元本と前年度までの利息の合計に対して当年度の利息が付く、という利殖の仕組みを反映した数値だ。ある銀行の外貨預金で、利率が1年目は30%、2年目は2%と、大きく変化したとしよう。このとき、2年間の平均利率は、いくらだろうか。算術平均の16%ではない。
元本として100万円を預けた場合で考えてみよう。1年後には、元本に30%の利子がついて130万円となった。2年後には、この130万円に2%の利子がついて、132万6000円に増加した。つまり、2年間で1.326倍に増えたわけだ。1年間でみると、1.326の平方根をとって、1.152倍ほどに増えることを意味する。つまり、平均利率は約15.2%となる。これは「幾何平均」と呼ばれる。
関連記事
 元日銀マンが斬る 厚労省の統計不正、真の“闇”
元日銀マンが斬る 厚労省の統計不正、真の“闇”
厚生労働省の「毎月勤労統計」が炎上している。これに関する不正をかばうものはいないだろう。誰の目に見ても明らかな不正である。しかしこの問題には深い「闇」があるのではないかという。 もしも銭形警部が人工知能を使いこなしたら、警察はルパンを逮捕できるのか?
もしも銭形警部が人工知能を使いこなしたら、警察はルパンを逮捕できるのか?
日本では「熱血型上司」が人気だという。しかし、近い将来それと対極にある存在が私たちの上司になるかもしれない。人工知能だ。そのとき、部下の動きはどのように変わっているのだろうか。「ルパン三世」の銭形警部を例に見ていこう。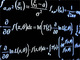 大人になったら使わないのに、なぜ私たちは「分数」を学ぶのか
大人になったら使わないのに、なぜ私たちは「分数」を学ぶのか
社会人になって「微分・積分や二次関数」を使ったことがある人は少ないはず。いや、ひょっとしたら、小学校の低学年で学ぶ「分数の足し算」も使ったことがないのでは。大人になっても使わないのに、なぜ私たちは「分数」を学んできたのか。その理由は……。 どれほど深刻? 厚労省不正統計問題を「超」分かりやすく解説
どれほど深刻? 厚労省不正統計問題を「超」分かりやすく解説
厚生労働省が作成する統計で、不正が行われていたことが波紋を呼んでいる。本記事では可能な限り分かりやすく、今回の統計不正について解説してみたい。 「ムダな会議」による企業の損失は年間15億円
「ムダな会議」による企業の損失は年間15億円
長時間労働や労働生産性について議論する際、しばしば指摘されるのが、「会議、打ち合わせの多さ」だ。果たして、日本企業はどのくらいの時間を会議に費やしているのだろうか……?
Copyright © NLI Research Institute. All rights reserved.
Special
PR注目記事ランキング


