病みつきになる「動的計画法」、その深淵に迫る：最強最速アルゴリズマー養成講座（3/4 ページ）

[高橋直大，ITmedia]

今回の問題

　今回は、TopCoderSRM383 Div1Medium問題からの出題です。

You are building a house and are laying the floorboards in one of the rooms. Each floorboard is a rectangle 1 unit wide and can be of any positive integer length. Floorboards must be laid with their sides parallel to one of the sides of the room and cannot overlap. In addition, the room may contain features such as pillars, which lead to areas of the floor where no floorboards can be laid. The room is rectangular and the features all lie on a unit-square grid within it. You want to know the minimum number of floorboards that you need to completely cover the floor.

You are given a String[] room containing the layout of the room. Character j in element i of room represents the grid-square at position (i, j) and will be a '.' if this square needs to be covered with a floorboard or a '#' if the square is a feature where no floorboard can be laid. Return an int containing the minimum number of floorboards you need to completely cover the floor.

Constraints

- room will contain between 1 and 10 elements, inclusive.

- Each element of room will contain between 1 and 10 characters, inclusive.

- Each element of room will contain the same number of characters.

- Each character in room will be a '.' or a '#'.

　これを適当に日本語に訳すと、以下のようになります。

何もないマスを「.」、障害物のあるマスを「#」で表現した部屋があります。障害物のあるマスは貫通できないものとして、何もないマスすべてを直線で横切りたい時、直線の本数の最小数を求めなさい。部屋の大きさは10*10以下とします。

　さて、この説明だけだとわかりにくいので、具体例を見ていきましょう。次のような文字列が与えられたとします。

{"...#.."
,"##...."
,"#.#..."
,".#...."
,"..#..."
,"..#..#"}

　これによって表わされる部屋は、以下のようなものです。

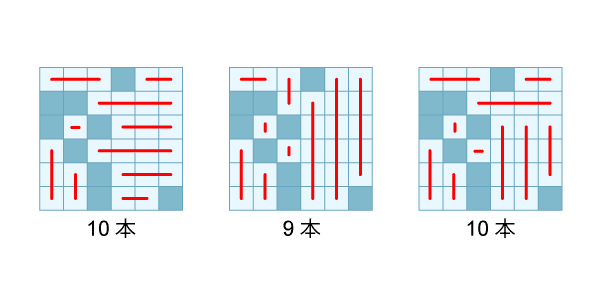
　この部屋に対して、直線を引いてすべてのマスを埋め尽くしたいとき、下図のように、さまざまな直線の引き方が考えられます。

　このように、直線ですべてのマスを埋め尽くす際に、最小の必要本数を求めるのが今回の問題です。

　今回の問題についても、取り組みやすいように、問題挑戦用のソースコードを用意しました。問題側で設定されたサンプルデータと、本当に正しいかどうかを検証するための凶悪なデータが後半にあり、それぞれ自動でチェック可能ですので、気軽に挑戦できます。C++、C#、Javaの3種類を用意しましたので、好きな言語で挑戦してみましょう。

ソースコードのダウンロードはこちらから

今回の問題のヒント

　動的計画法やメモ化再帰に慣れている人は、この問題も即座に解けるでしょうが、慣れていない人には、手のつけようのない問題かと思います。

　この問題で大切なのは「どのように探索するか」です。やみくもに引ける直線を片っ端から引いていったとしても、恐らく探索は可能です。しかし、最大10*10の部屋に対して、直線の引き方は無数に存在しますし、これをすべて探索しきるのは不可能です。よって、柔軟な発想が必要となります。

　ここで必要となるのは、まず「順番に探索すること」です。上の行から順番に直線を引いていけば、重複なくすべての通りを探索することは、小さいサイズであれば問題なく行えるでしょう。さらにもう1つ、つながっているからといって、まとめて考えることはない、というのも大切です。例えば長さが2つ分の横棒があったとしても、これは1本の横棒が2つ並んでいる、と見ることも可能です。この2つは、探索をする際に大切なテクニックとなります。

　ここまで分かれば、後は「どのようにその結果を記憶させ、無駄な計算を省くか」です。ここが動的計画法などの肝となる部分で、これが思いつけるようになれば、動的計画法マスターに1歩近づけるのではないかと思います。