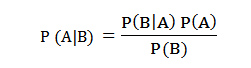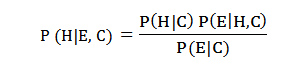ベイズの理論が変える「確率」の使い方:「ベイズな予測」で未来を拓け(1)(1/2 ページ)
量子力学などの最先端科学分野では、統計学の客観的確率では説明がつかない矛盾が生じ始めている。ここでは「主観的確率」について研究する「ベイズの理論」について、マイクロソフトのシニアテクニカルアーキテクト、宮谷隆氏に解説してもらう。
書籍『ベイズな予測』で紹介しているベイズ確率は、統計学から生じたものではなく、確率の研究にはじまり、計算機科学、特にデータマイニング技術によって発展してきたのは歴史的な事実である。主に予測に使われてきた。量子力学など幾つかの最先端科学分野では、統計学の客観的確率では説明がつかない矛盾が生じてしまうと言われ始めており、客観的確率の限界がそこかしこで見られ始めている。既に先端科学技術分野では、もっぱら主観的確率が使われるようになってきている。
まずはベイズの定理だが、250年間も統計学者に相手にされなかったものである。ちょっと前と異なり、最近よく見かけるベイズの定理は、下記のように表現されている。
しかし本当に、こんな数式が250年間も封印されてきたのだろうか?
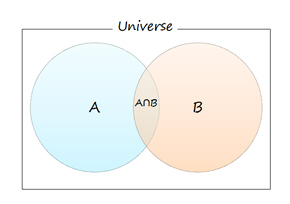
この数式であれば、ベン図を使うと非常に分かりやすく説明できる。ここに集合Aと集合Bがある。全体に対する集合Aの割合と集合Bの割合が分かっている。AとBの両方の集合に属しているのは集合ABである。集合Aに対する集合ABの割合も分かっている。このときに集合Bに対する集合ABの割合は何%になるか求められると解釈できる。
例えば、インフルエンザの疑いがある100人の患者がいるが、新型インフルエンザに感染している患者数は明らかになっており、これを集合Aとする。同じ100人に簡易検査を行った場合、陽性となる数も分かっており、これを集合Bとする。集合ABは、簡易検査の結果、陽性となった新型インフルエンザ患者である。
・集合A:新型インフルエンザ患者
・集合B:簡易検査で陽性となった患者
・集合AB : 簡易検査で陽性となった新型インフルエンザ患者
集合Aの中で、集合ABに属する患者数も分かっている。これを表すのがP(B|A)だ。新型インフルエンザの患者が簡易検査で陽性になったかどうかの割合である。この式で求めようとしているP(A|B)とは、これとは逆だ。簡易検査で陽性となった患者が新型インフルエンザ患者かどうかの割合を表す。いわば新型インフルエンザに対する簡易検査の有効性といったところだ。
ここで、問題そのものに疑問を持ちたい。集合A、集合Bと集合ABの数が分かっているという前提である。であれば、集合ABの患者数を集合Bの患者数で割ればP(B|A)はすぐに得られる。回りくどい数式を使う必要はないのだ。もともと徹底した検査結果なのだから、P(A|B)は明らかな状況であり、問題にならないのではないか、という単純な疑問だ。さらなる疑問は、こんな単純な数式が250年間も否定され続け、つい最近まで、学術分野ではまともに相手にもされなかったことだ。そんな事があり得るのだろうか?
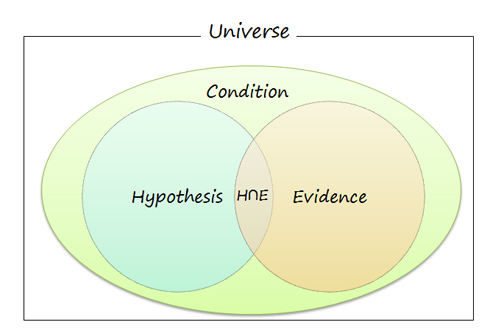
わたしが書籍「ベイズな予測」で紹介した「ベイズの定理」は、上記の式に展開は可能だが異なる数式である。インターネットでも、注意深くトーマス・ベイズを調査するとこの数式を見つけることができるだろう。
この式でのHは、仮説(Hypothesis)である。Eは証拠(Evidence)であり、Cは、状態、条件(Condition)である。数式を言葉で言い換えれば、「ある状態においての仮説に対する確率は、状態の変化に伴う条件付き確率で、確率を向上させることができる」と解釈してよい。
これはまさに、人間がある物事に対しての主観的な確信について、確証の度合いを評価するのに似ている。
- AさんとBさんは同じ会社で同じプロジェクトに参加している。(状態)
- AさんとBさんが付きあっている、といううわさがある。(仮説)
- 渋谷の交差点で夜2人が歩いているのを見かけた。(証拠)
これにより、主観的には仮説に関する確信の度合いが高まったといえる。
最初に説明した式との決定的な違いは、HもEも確定していない状態だという点である。H(仮説)は確定したものではない。E(証拠)は新たな証拠の提出によって変化する。だが本当に興味深いのは、予測する確率が新しい情報により向上するという部分だ。ベイズの定理が、神の存在をも予測できる、といわれるゆえんである。
Copyright © ITmedia, Inc. All Rights Reserved.
アイティメディアからのお知らせ
人気記事ランキング
- 知らない番号でも一瞬で正体判明? 警察庁推奨アプリの実力を検証
- ZIPファイルの“ちょっとした細工”で検知停止 EDRも見逃す可能性
- M365版「Cowork」登場 Anthropicとの連携が生んだ「新しい仕事の進め方」
- 生成AIで消えるのは仕事、それとも新人枠? 800職種のデータから分かったこと
- AD DSにSYSTEM権限取得の脆弱性 Microsoftが修正プログラムを配布
- 偽のTeamsサポートで新型バックドアを設置 巧妙な手口に要注意
- .NETにサービス停止の脆弱性 広範なアプリケーションに影響
- もはやAIは内部脅威? 企業の73%が「最大リスク」と回答
- 政府職員向けAI基盤「源内」、18万人対象の実証開始 選定された国産LLMは?
- 本職プログラマーから見た素人のバイブコーディングのリアル AIビジネス活用の現在地