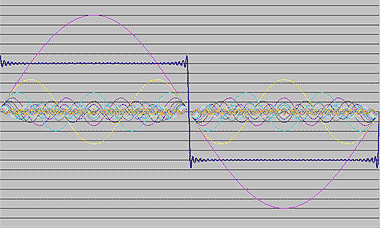
OFDMとは何か? 1 :塩田紳二のモバイル基礎講座 第7回: (3/3 ページ)
|
次回は、OFDMを利用するメリットや、変調・復調の仕組み、また、位相変調とグレイコードについて説明します。
関連記事
- 塩田紳二のモバイル基礎講座 第6回:電波で情報を送れる仕組み 2
前回お話したように、無線で通信ができるのは「変調」という技術のおかげです。今回は無線LANやBluetooth、CDMA方式の携帯電話などで採用されている変調方式について解説します。 - 塩田紳二のモバイル基礎講座 第5回:電波で情報を送れる仕組み 1
無線で通信ができるのは、伝えたい情報を電波に載せる「変調」という操作のおかげです。ASK、FSK、PSKなどの変調方式のほか、より多くの情報を送るためのQPSK、16QAMなどについても解説します。 - 塩田紳二のモバイル基礎講座 第4回:そもそも電波って何だろう 2
電話を少し動かしただけで電波の受信状態が変わる理由、ダイバシティアンテナとは何をするものか、偏波とは何か──前回に引き続き、電波についてお話しします。 - 塩田紳二のモバイル基礎講座 第3回:そもそも電波って何だろう?
携帯電話は電波を使って通信しています。しかしそもそも電波とは何なのでしょうか? 最近話題に上ることが多い“周波数帯”についても解説します。 - 塩田紳二のモバイル基礎講座 第2回:日本の2G携帯電話
日本の2G携帯電話は、NTTドコモやボーダフォン、ツーカーが採用しているPDCと、KDDIが採用しているcdmaOneとに分けられます。今回は2つの違いについて見ていきましょう。 - 塩田紳二のモバイル基礎講座 第1回:2G、3Gの「G」とは何を指す?
本連載では「モバイル基礎講座」と題して、通信やコンピュータなどに関する気になる用語を取り上げ、分かりやすく解説していく。第1回目で取り上げるのは“3G携帯”などというときの「G」だ。
Copyright © ITmedia, Inc. All Rights Reserved.
Special
PR注目記事ランキング