会計原価を損得計算に使うな！（2）：システム部門Q＆A（21）（1/2 ページ）

前回は、損得を考える際には「比較の原則」と「余裕有無の原則」が必要であることを示した。これらの法則を考慮した損得原価を求める最適化技法に、LP（Linear Programming：線形計画法）がある。今回は、通常の原価計算とLPの違いを説明する。

[木暮 仁，＠IT]

質問

管理会計やLPも損益計算に使えるのでしょうか？

前回では「損得計算では比較の原則と余裕有無の原則が重要なので、会計原価は使えない」ということを理解しました。ところで、こういった考え方には管理会計もありますし、学生のときにLPとやらを聞きかじったことがあります。これらは損得計算に使えるのでしょうか？

意見

管理会計やLPも損益計算に使えるのでしょうか？

　「余裕有無の原則」を用いた最適化手法に、LP（Linear Programming：線形計画法）があります。今回は、LPの数学的意味や解法には深入りはせず（これらに関しては、「線形計画法の概要」などを参照してください）、通常の原価計算の考え方とLPの違いを示すことで損得計算への理解を深めたいと思います。

会計原価とLP

　前回は、損得を考える際には「比較の原則」と「余裕有無の原則」が必要なことを理解しました。これらの法則を考慮した損得原価を求める最適化技法に、LP（Linear Programming：線形計画法）があります。今回は通常の原価計算とLPの違いを示すことにより、損得計算への理解を深めたいと思います。

　　　　　（1）例題　　　　　　

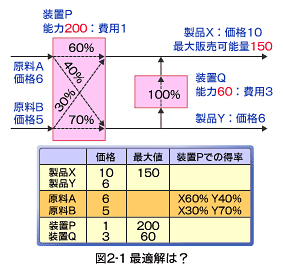
　次のような製品、原料、装置があります。

　このとき、原料Aと原料Bはどちらが有利でしょうか？ それを通常の原価計算の方法で評価しましょう。

○原価計算1

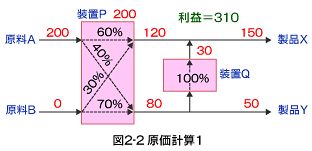
　原料Aを1トン用いて装置Pで1トン処理すると、その費用は6円＋1円＝7円になります。そして、製品Xが0.6トン、製品Yが0.4トンでできるのですから、売り上げは0.6×10＋0.4×6＝8.4円になり、利益は8.4円−7円＝1.4円になります。同様に、原料Bが1トンの場合では、売り上げ＝0.3×10＋0.7×6＝7.2円、費用＝5＋1＝6円で、利益＝1.2円になります。その結果、原料Aの方が有利となります。

　そこで、原料Aを装置Pの最大能力200トンを用いて製品Xを最大限に生産すると、利益は310円になります。

○原価計算2

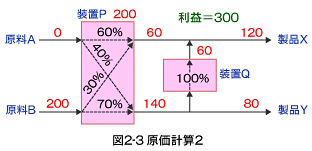
　装置Pの出口の上の部分は、製品Xの価格を適用すれば10円です。下の出口ですが、それを6円の製品Yにするよりも3円掛けて装置Qで処理し、10円の製品Xを作る方が有利ですから、そのように考えると、10−3＝7円になります。この数値を用いて原価計算1と同様の計算をすると、

・原料A：（0.6×10＋0.4×7）−（6＋1）＝1.8円

・原料B：（0.3×10＋0.7×7）−（5＋1）＝1.9円

　となるので、原料Bの方が有利となり、原料Bを200トン用いたときの利益は300円になります。

○LPによる計算

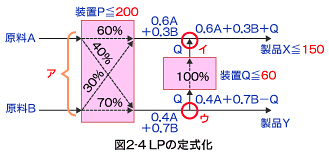
　LPでは、次のように定式化します。

制約式
A＋B＝P	……ア
0.6A＋0.3B＋Q＝X	……イ
0.4A＋0.7B−Q＝Y	……ウ
0≦X≦150　 0≦Y
0≦A　　　　　0≦B
0≦P≦200　 0≦Q≦60

の制約式の下で、目的関数

10X＋6Y−6A−5B−1P−3Q→max

を最大にする、変数X、Y、A、B、P、Qを求める。

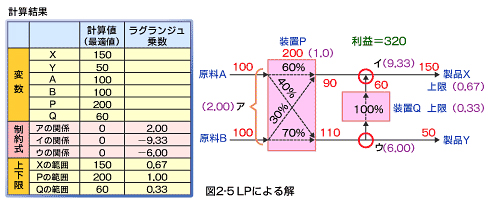
　この解法は省略しますが、最適解は原料Aが100トン、原料Bが100トンのときに、利益（目的関数の値）は320円になります。

	原料A	原料B	利益
原価計算1	200	0	310
原価計算2	0	200	300
LPの解	100	100	320

　原価計算の結果がLPの解よりも利益が低くなった理由は、LPはすべての条件を同時に満足させて最適化を図っているのに対して、原価計算ではその一部しか考慮していない（製品Xや装置Qの制約など）ので、部分最適になっているからです。

　ここで問題なのは、原価計算を信奉している人は、もっと良い解があることに「気付いていない」ことです。知らないうちに損をしているのですね。