アルゴリズマーの登竜門、「動的計画法・メモ化再帰」はこんなに簡単だった:最強最速アルゴリズマー養成講座(1/5 ページ)
動的計画法・メモ化再帰というと難しいアルゴリズムであるかのように聞こえますが、実際には小学生でも分かるほど簡単なアルゴリズムです。使用できるメモリと実行時間を意識しながら、同じ計算をする無駄を省くことができれば、かなりの実力者となれます。
この記事は会員限定です。会員登録すると全てご覧いただけます。
動的計画法とメモ化再帰
今回は、非常によく用いられるアルゴリズムである、「動的計画法」「メモ化再帰」について説明します。この2つはセットで覚えて、両方使えるようにしておくと便利です。
なお、メモ化再帰に関しては、第5・6回の連載の知識を踏まえた上で読んでいただけると、理解が深まります。まだお読みになっていない方は、この機会にぜひご覧ください。
では、簡単な問題を例に挙げて解説していきましょう。
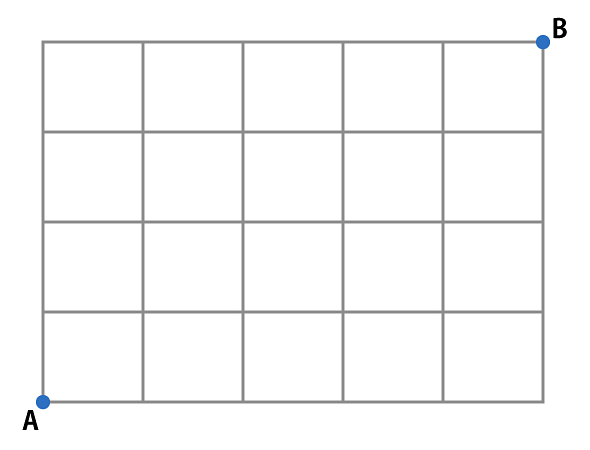
下図のような格子状の道があります。A点からB点に向かって遠回りせずに移動したいとき、移動する経路は何通りあるでしょう?
中学受験などを経験された方であれば、こういった問題を一度は解いたことがあるのではないでしょうか。小学校の知識までで解こうとすれば、少し時間は掛かるかもしれませんが、それでもこれが解けないという方は少ないだろうと思います。
この問題をプログラムで解こうとすると、さまざまな解法が存在します。解き方によって計算時間や有効範囲が大きく変化しますので、それぞれのパターンについて考えます。
以下の説明では、縦h、横wとして表記し、プログラムの実行時間に関しては、TopCoderで使用可能な言語であればだいたいこれくらい、という表記を行っています。計算量の「オーダー」については、連載第2回「オーダーを極める思考法」で解説していますので、ご存じない方はまずそちらをご覧ください。
探索による全列挙
まずは、コンピュータ上で行う操作を考える上で、一番よく用いられる、力ずくでの探索について考えてみましょう。やり方は簡単で、左下からスタートし、順番に指でなぞって何通りあるか調べるだけです。連載第5回で説明をした深さ優先探索です。この問題は、答えを書いてしまうと126通りなのですが、これをコンピュータにやらせると、これくらいのサイズであればすぐに解が求まります。
しかし、これが大きなサイズになるとそうもいきません。計算量を考えると、右に行くか上に行くかの選択をh+w回行うことになるので、ざっとO(2^(h+w))程度の計算量となります。2^30でだいたい10億ですので、たった15×15程度のサイズでも、かなりの時間が掛かってしまうことが予想できるわけです。これでは少し遅いので、別の方法を考えてみましょう。
数学的解法
次に、数学的解法で考えてみます。上述の問題は、「右に5回、上に4回移動する方法が何通りあるか」ということになります。これを読み替えると、「合計9回右か上へ移動をするとき、上へ4回移動するパターンは何通りあるか」となります。ここまで分かっていれば、2項定理を利用して、9C4=126通り、と簡単に求めることができます。
この場合の計算量は、単なる組み合わせの数を求めるだけですので、O(h+w)という非常に小さな計算量となります。実際にはけたあふれの問題が発生するのですが、実行時間を考えれば、h、wがそれぞれ100程度と考えた時に、探索では何年経っても終わらないような計算を、1ミリ秒以下程度と、ほとんど一瞬で終わらせることが可能です。厳密には、そこまでの広さの範囲で考えると、答えが莫大な数になり、整数で表わすのは困難になりますが、ここではそこまで考えないものとします。
上述の問題に関しては、この解法で十分なのですが、数学的解法は、少しでもイレギュラーが発生してしまうと対応できなくなるケースがあります。例えば、下図のように、通れない点が発生したとします。
最初に示した探索での方法であれば、そこを通らなくすればよいだけですので、簡単に対応できますが、二項定理を使った方法の場合、例外処理、といった形で対応しなければならず、通れない点が増えた場合には手に負えなくなります。
このように、数学的に解いた解法は、美しいのですが、わずかなイレギュラーが発生してしまった瞬間に使えなくなることが多いのです。これまで本連載では数学的にきれいな解法を連続して紹介してきましたが、そういった方法が必ず有効とは限りません。そこで登場するのが、今回紹介する動的計画法やメモ化再帰なのです。
Copyright © ITmedia, Inc. All Rights Reserved.
アイティメディアからのお知らせ
人気記事ランキング
- 知らない番号でも一瞬で正体判明? 警察庁推奨アプリの実力を検証
- ZIPファイルの“ちょっとした細工”で検知停止 EDRも見逃す可能性
- M365版「Cowork」登場 Anthropicとの連携が生んだ「新しい仕事の進め方」
- 生成AIで消えるのは仕事、それとも新人枠? 800職種のデータから分かったこと
- AD DSにSYSTEM権限取得の脆弱性 Microsoftが修正プログラムを配布
- 偽のTeamsサポートで新型バックドアを設置 巧妙な手口に要注意
- .NETにサービス停止の脆弱性 広範なアプリケーションに影響
- もはやAIは内部脅威? 企業の73%が「最大リスク」と回答
- 政府職員向けAI基盤「源内」、18万人対象の実証開始 選定された国産LLMは?
- 本職プログラマーから見た素人のバイブコーディングのリアル AIビジネス活用の現在地