病みつきになる「動的計画法」、その深淵に迫る:最強最速アルゴリズマー養成講座(1/4 ページ)
数回にわたって動的計画法・メモ化再帰について解説してきましたが、今回は実践編として、ナップサック問題への挑戦を足がかりに、その長所と短所の紹介、理解度チェックシートなどを用意しました。特に、動的計画法について深く掘り下げ、皆さんを動的計画法マスターの道にご案内します。
もしあなたが知ってしまったなら――病みつきになる動的計画法の集中講義
前回の『アルゴリズマーの登竜門、「動的計画法・メモ化再帰」はこんなに簡単だった』で動的計画法とメモ化再帰を説明しましたが、前回の説明ではまだ勘所をつかめていない方がほとんどでしょう。そこで、これらを完全にマスターするため、今回はもう1つ具体例を挙げながら練習したいと思います。
どういった問題を採用するかは悩みましたが、非常に有名な「ナップサック問題」を取り上げて説明します。
ナップサック問題とは以下のような問題です。
幾つかの品物があり、この品物にはそれぞれ重量・価値の2つのパラメータが与えられています。ある一定の重さまで品物を運べるとしたときに、価値の合計の最大値は幾つになるでしょう?
これでは少し分かりにくいので、問題を具体例にしてみましょう。重さが合計10まで運べるとして、以下のように重量と価値が異なる幾つかの品物があるとします。
| 品物 | A | B | C | D | E |
|---|---|---|---|---|---|
| 重量 | 3 | 4 | 1 | 2 | 3 |
| 価値 | 2 | 3 | 2 | 3 | 6 |
では、これを動的計画法を用いて解いてみます。前回取り上げた問題では、「縦」「横」という2つの要素に対して「そこまで行くのに何通りの方法があるか」を格納しましたが、今回は、「合計の重さ」と「何番目の品物まで考えたか」という2つの要素に対し、「価値の合計の最大値」を格納します。これ以外にも方法はありますが、ひとまずはこれで考えてみましょう。
まず、0番目まで考慮した場合ですが、これは要するに「何も品物がない状態」を表しますので、品物は当然重さ0、価値0しか存在しません。よって、下図のようになります。
次に、品物Aについて考えます。1つ前までの品物を考えた時の重さごとの最高価値が分かっているので、それに対して今度考える品物を運ぶ/運ばないで場合分けして考えればよいということになります。品物Aが重量3、価値2であることを考慮すると、下図のように表すことができます。空欄部分は、存在し得ない組み合わせだということになるので、この時点では無視しましょう。
次に品物Bに関しても考えてみましょう。品物Bは重量4、価値3です。これも先ほどと同様の処理をするだけなので、下図のようになります。
徐々に増えてきましたが、さらに品物Cに関しても考えてみます。品物Cは重量1、価値2です。ここでようやく、重さ4の地点で、2つの矢印が重なる場面が発生しました。こういった場合、今回は「価値を最大にする」のが目的なので、数字が大きくなる方を選びます。
これを最後の品物まで試すと、以下のようになります。
これで、最後の品物まで考慮した際の、ある重さにおける価値の最大値を求めることができました。この表によると、重さ10以下の時の最大値は14なので、答えは14だと分かります。もし、どの品物を運ぶべきかまで知りたい場合は、答えの数値から矢印をたどって逆算することで、どれを使ったかが調べられます。ここまで、かなりあっさりと説明しましたので、分からない場合もあるかもしれませんが、それほど難しいことは説明していませんので、落ち着いてゆっくり読み直してみてください。
前回も動的計画法を説明しましたが、今回の解説を見て、「全然前回と違うじゃないか」と思っている方も多いかもしれません。しかし、これも構造上は前回と同じなのです。
前回はきれいな格子状に道がつながっていましたが、今回は、「品物を運ぶ道」と「運ばない道」の2つの道が各マスから出ているだけです。また、前回は「何通りあるか」を数え上げる必要があったので、数字を足し合わせていましたが、今回は「価値を最大にする」ことを目的にしているので、数字の最大値を取っています。それ以外はまったく同じです。
このように、問題に合わせて計算の仕方を変えるだけで、さまざまな問題に対応できるのも動的計画法の強みです。狭い定義では当てはまりませんが、『知れば天国、知らねば地獄――「探索」虎の巻』で紹介したダイクストラ法なども、動的計画法のような考え方を利用しており、非常に応用が利くアルゴリズムです。
Copyright © ITmedia, Inc. All Rights Reserved.
アイティメディアからのお知らせ
人気記事ランキング
- VS Code拡張機能4件に重大な脆弱性 累計ダウンロード数は1.2億
- 富士通、開発の全工程をAIで自動化し「生産性100倍」 自社LLMのTakaneを活用
- Chromiumにゼロデイ脆弱性 悪用コードが流通済みのため急ぎ対処を
- 悪いのは本当にVPN? 日本医科大武蔵小杉病院のランサムウェア事件をダークWebから解明
- 関西電力が「AIファースト企業」化に本気 脱JTCを図る背景と全従業員“AI武装化”の全貌
- SMBC日興証券が「パスキー」で口座乗っ取り対策 約5カ月で実現したのはなぜ?
- ドローンいらず? 飛行動画作成できる「Google Earth Studio」登場
- 「英数・記号の混在」はもう古い NISTがパスワードポリシーの要件を刷新
- アサヒGHDがランサムウェア被害の調査報告書を公開 152万の個人情報が漏えいの恐れ
- そのセキュリティ業務、自前と外注のどちらが正解? 勘に頼らない判断のこつ
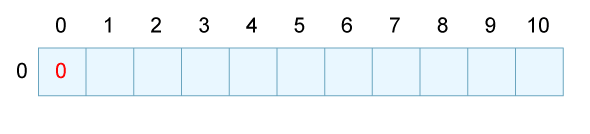
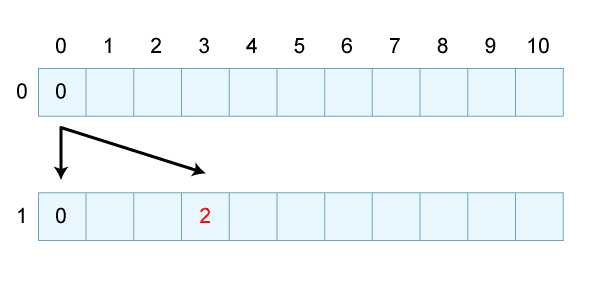 重量3、価値2の品物Aを考慮した図
重量3、価値2の品物Aを考慮した図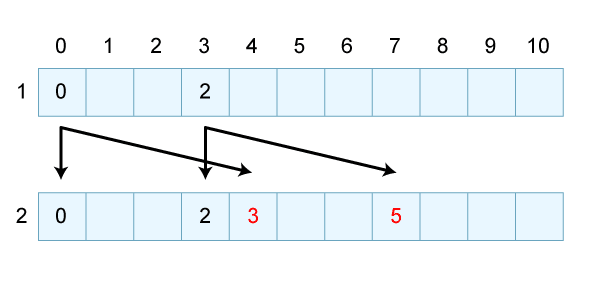 品物Bは重量4、価値3なので、このように表すことができる
品物Bは重量4、価値3なので、このように表すことができる 重量1、価値2の品物Cまで考えたところ
重量1、価値2の品物Cまで考えたところ 品物すべてについて試したもの
品物すべてについて試したもの