そのアルゴリズム、貪欲につき――貪欲法のススメ:最強最速アルゴリズマー養成講座(1/3 ページ)
アルゴリズムの世界において、欲張りであることはときに有利に働くことがあります。今回は、貪欲法と呼ばれるアルゴリズムを紹介しながら、ハードな問題に挑戦してみましょう。このアルゴリズムが使えるかどうかの見極めができるようになれば、あなたの論理的思考力はかなりのレベルなのです。
動的計画法は本当に万能なのか?
本連載ではこれまで、かなりの文量を割いて動的計画法について説明してきました。動的計画法はさまざまな問題で有効な解決手段ですが、動的計画法が使えるからといって、常に動的計画法を利用することが正しい選択である、というわけではありません。この理由は簡単で、動的計画法は計算量を大幅に削減できますが、その本質は、不要である要素を切り捨てることで問題全体を見渡すというアルゴリズムであるためです。
ここで問題となるのが実行速度です。もし、問題全体を見渡さずに、今の状態だけを見て次の選択肢を選んでしまうような、そんなアルゴリズムで最適解が得られてしまう場合、これらのアルゴリズムは動的計画法を利用するよりもはるかに早いものとなり得ます。つまり、動的計画法が適用できるからといって、ノータイムでそれを選択するというのは早計である、ということになります。
これを理解するため、前回のチェックシートから1問再掲します。
100万円以下の金額が入力される。この金額を日本の硬貨・紙幣で支払うとき、支払う合計枚数の最小値を出力しなさい
この問題を、動的計画法以外の方法で解けるのではないか? と考えた方は多いでしょう。実際、前回のチェックシート掲載時にも10件以上の問い合わせがありました。次に繋がる話となりますので、時間と手間を掛けて消化していただければと思います。
上述の問題を動的計画法で解こうとすれば、前回解説したナップサック問題とほとんど同じ方法で解くことができます。この問題では、存在する貨幣の価値は、{1,5,10,50,100,500,1000,2000,5000,10000}と表せますので、0円から求める金額までの間を、前回とほぼ同じ要領で埋めていけばよいだけです。
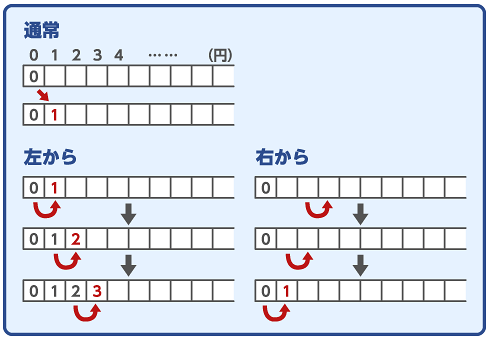
ナップサック問題では1つの商品は1回しか使えませんでしたが、こちらの問題では1種類の硬貨を何度も使える点が差異となっています。前回は配列を2つ用意して更新していましたが、下図のように、これを1つにまとめ、左から更新していけばこの差異に対応できます。なお、右から更新していくことで、前回と同様1回だけの利用に制限することもできます。よく分からない場合は、前回の記事と見比べながら、じっくり考えてみてください。
こうして動的計画法を用いれば、計算時間はO(金額×貨幣の種類数)となり、100万円程度であれば、1秒以内で解くことができます。ここまでが前回の復習で、ここから新しい内容に入っていきます。
なじみ深いようで意外と難しい「貪欲法」
ここまでの解説で、違和感を覚えた方はどれくらいいるでしょうか。もう皆さんお気付きでしょうが、1万円以上の品物を買うのであれば、まずは1万円札を払えるだけ払うのが自然です。それ以下の金額も同じように、使用可能な貨幣のうち一番金額の高いものを使っていくことで、簡単に最適な方法を求めることができます。こういったアルゴリズムを「貪欲法(Greedy Algorithm)」と呼びます。「欲張り法」という呼び方をされることもありますが、両者は同じものを指します。
貪欲法と言ってもかなり幅が広いのですが、多少強引にまとめると、「適当な基準を用いて、局所的に最適なケースを連続して選択する」だけのアルゴリズムです。言い換えれば、目先の解が最適なものであればよいという文字通り貪欲な探索手法であるといえます。
これを聞くと、これまで紹介してきた動的計画法の解法は、一見無意味に思えるかもしれません。貪欲法の方が単純で分かりやすく、しかも計算時間は非常に短いのですから。
ただし、上記の問題を貪欲法で解こうとすると、意外と難しいことに気がつくと思います。なぜなら、「貪欲法で最適な答えが求まる保証がない」ためです。
なじみ深い日本の貨幣のセット{1,5,10,50,100,500,1000,2000,5000,10000}であれば、感覚的に明らかにそうである、と自信を持って言えるかもしれません。では、例えばこれが米国の貨幣だったらどうでしょうか? 貨幣セットを上記と同じように表現すると、{1,5,10,25,50,100,200,500,1000,2000,5000,10000}となります。これでも同じように、できるだけ大きい貨幣から使えば最適解が得られる、と主張できるでしょうか? 恐らく多くの人が自信をなくしてしまうのではないかと思います。
もう少し極端な例として、オリジナルの貨幣セットとして{1,4,7}の3種類しかないときと、{1,6,13}の3種類しかないときの2通りを考えてみましょう。この場合でも貪欲法で最適解は得られるでしょうか? 実はこの2つの場合、前者の{1,4,7}のセットは貪欲法で最適解を求めることができます。しかし、{1,6,13}の場合は、最適な解を求めることができません。
例えば18円を支払わなければならない場合、大きい順から支払っていくと、13、1、1、1、1、1の6枚になりますが、実際には6、6、6の3枚が最適な解です。このように反例を見つけることが簡単にできるのです。
ここまでをまとめると、「貪欲法を用いて最適解が導けるケース」と「貪欲法では近似解しか導けないケース」の2通りが存在し、どちらであるかを見極めることは簡単ではないことも多いというわけです。
コンテストにおける貪欲法の使い方
実は、上記の問題については、貨幣の種類数Nに対して、O(N^3)で、貪欲法で答えが導けるかを検証するアルゴリズムが存在します。しかし、そこまで時間を掛けて検証していては、短時間のコンテストで戦うことなどできません。
とはいえ、貪欲法は非常に高速かつ実装が簡単なことが多いので、見極めがうまくできるなら積極的に利用したいアルゴリズムです。そこで、貪欲法を利用するべきかどうかを判断する思考の流れについてまとめました。これはコンテストでも有効な思考法です。
- 貪欲法を用いて最適解が明らかに求まる、もしくは簡単な証明で求まる(or 求まりそうな)場合、貪欲法を即座に使用する
- 貪欲法が使用可能かどうか疑わしい場合で、ほかのアルゴリズムを用いて答えを求めることができる場合、ほかのアルゴリズムを用いる
- 貪欲法以外の解法で時間内に解ける方法が思い浮かばない場合、貪欲法で最適解が求まらない反例を探し、それが見つからない場合は貪欲法で実装してみる
この辺りの判断は、数学的な直感力や証明力などが影響することが多いので、苦手な方もいるでしょう。また、経験も多分に影響しますので、コンテストなどに実際に参加しながら、正しい判断が下せる確率を高めていけばよいと思います。
それでは、次のページから、実際に出題されている問題に移ります。
Copyright © ITmedia, Inc. All Rights Reserved.
アイティメディアからのお知らせ
人気記事ランキング
- SMBC日興証券が「パスキー」で口座乗っ取り対策 約5カ月で実現したのはなぜ?
- 初期侵入口は“またVPN” 日本医大武蔵小杉病院にランサムウェア攻撃
- 悪いのは本当にVPN? 日本医科大武蔵小杉病院のランサムウェア事件をダークWebから解明
- 生成AIの記憶機能を悪用して特定企業を優遇 50件超の事例を確認
- 日本IBMのAI戦略“3つの柱” 「制御できるAI」でレガシー資産をモダナイズ
- アサヒGHDがランサムウェア被害の調査報告書を公開 152万の個人情報が漏えいの恐れ
- 「2027年1月12日」は運命の日? サポート切れOSを使い続ける会社の末路
- 人材水準を4段階で評価 「サイバー人材フレームワーク」案の意見公募を開始
- 「英数・記号の混在」はもう古い NISTがパスワードポリシーの要件を刷新
- 「AI前提」の国家戦略と「思考停止」の現場 大半の企業で“何も起きない”未来を予見