知れば天国、知らねば地獄――「探索」虎の巻:最強最速アルゴリズマー養成講座
いよいよ今回から、具体的なアルゴリズムの紹介に入っていきます。今回は、プログラミングにおける重要な概念である「探索」について考えます。グラフに変換し、探索する、という流れを知るとともに、そのグラフを効率よく探索する方法について紹介します。
今後紹介していくアルゴリズムについて
お待たせしました! 「最強最速アルゴリズマー養成講座」という連載タイトルのとおり、今回の連載からいよいよ具体的なアルゴリズムの紹介に入っていきたいと思います。
しかし、それを読んでいただく前に、1つ注意してもらいたいことがあります。連載第3回でもお伝えしたように、「問題を、既存の適当なアルゴリズムに当てはめる」という考え方は、非常に危険である、ということです。
筆者の経験上、TopCoderでRedCoder以上を目指すのであれば、回答時間短縮のために、いままでのパターンを利用するのも方法の1つなのですが、本連載では、発見的な視点を育てていただきたいので、単にアルゴリズムを覚えればよいというものではなく、「できるだけ頭を柔らかくして考える」ことを心掛けてください。
なお、アルゴリズムの紹介は、比較的あっさりとしたものにとどめたいと思います。こうしたものは目で見るより、実際に手を動かして学ぶのが有効であると筆者は考えるからです。手を動かすための動機付けは、今後の連載で補っていこうと思っていますので、まずは気楽に読み進めてください。
幅優先探索と深さ優先探索
プログラミングにおいては、「探索」という概念が必要になります。では、プログラミングにおける「探索」とは何でしょうか? ここでは具体例として、「幅優先探索」と「深さ優先探索」を考えてみましょう。
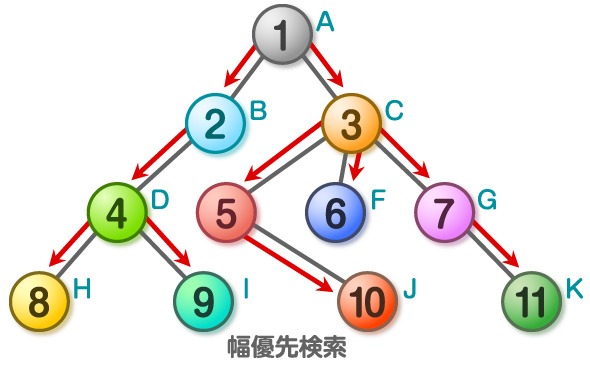
まず、幾つかの用語を説明しておきます。上図に出てくる丸を「頂点(ノード)」、それらを結ぶ線を「辺(エッジ)」と呼びます。連載第1回でも少し触れましたが、このように、頂点と辺で表されている構造を「グラフ」と呼びます。また、図のように、頂点と辺で「ループ(1周できる部分)」がなく、すべての頂点がつながっている構造を、「木構造」と呼びます。
上図の頂点Aから、数字の小さい順番に頂点をたどっていきます。このように、順番にたどる行為が「探索」と呼ばれるものです。
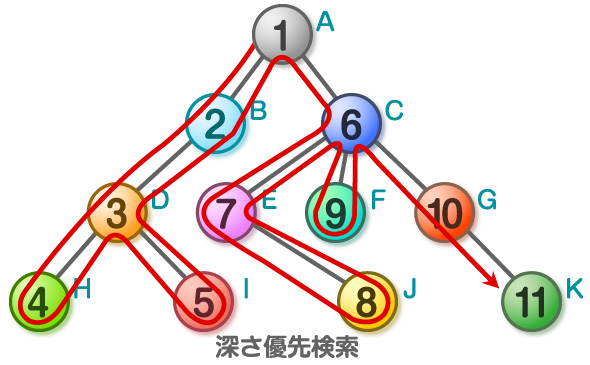
見た通りですが、「幅優先探索」は、深さの浅い点(頂点Aからたどる辺の数が少ない点)から順番に、また、左側にある頂点から順番に、というルールの下で探索しています。一方、「深さ優先探索」では、とにかくなるべく左に深く進むというルールで探索しています。子のないノード(例えば頂点H)まで探索した後は、最も近くの探索の終わっていないノード(ここでは頂点D)まで戻り、探索を行っています。
この2つの探索の違いですが、幅優先探索では、前回調べた頂点から1つ先の頂点をすべて調べるという行為を繰り返すものなので一筆書きができません。深さ優先探索は、前にいた点から次の点、というように探索していくので、一筆書きができる、という違いがあります。
これらの探索が何の役に立つのかということは、問題を解いてゆくうちにつかめてくるとは思いますが、幾つか具体例を挙げてみると、例えば以下のようなものがあります。
- 頂点Aは、幾つの頂点と直接的または間接的に接続しているか?
- 頂点Aから頂点Jに移動することは可能か? 可能だとすれば、どのように移動するのか?
- 上から下の向きにのみ移動できるとして、頂点Aから、順に移動できなくなるまで移動するとき、何通りの行き方があるか?
上述した具体例のうち、1つ目、2つ目の例のように、辺をどちら向きにも移動してよい場合と、3つ目の例のように、辺を移動してよい向きが決められている場合があります。どの辺も、好きな方向に移動してよいグラフのことを「無向グラフ」、一方通行がどこかに存在するグラフのことを、「有向グラフ」と呼びます。こうしたものが出題の条件として書かれていることもありますので、注意してください。
たいていの事柄はグラフに変換できる、よろしい、ならば探索だ
ここで、「グラフの探索順って現実の問題とどう結びつくの?」と不思議に思われる方もおられるかもしれません。実際、筆者の知る限り、グラフに変換できないものには、探索を使うことはできません。しかし、ここが重要なのですが、「たいていの事柄はグラフに変換できる」のです。
例えば、ボードゲーム、ここでは将棋を考えます。まず初期状態があり、これを頂点とします。それから、次の一手を列挙し、これを辺と考えます。その手を打った際に発生する次の盤面を、また新しい頂点と考えます。そこからの次の1手を、また辺として列挙していきます。このようにして、盤面の状態1つ1つをグラフの頂点、手の1つ1つを辺と考えます。このようにすることで、将棋を巨大な有向グラフだと考えることができるのです。それにより、探索による先読みが可能になるわけです。
要は、問題をグラフとしてうまく表現できれば、あとはそのグラフを効率よく探索する方法を考えればよいのです。プログラムは、特定の決められた法則に従って探索することしかできません。これは、言い換えれば、法則を定め、その法則をプログラムで表現できれば、どのような順番でも探索が可能である、ということになります。
もちろん探索には幅優先探索や深さ優先探索といった比較的単純なもの以外に、もっと高度な探索方法もあるのですが、幅優先探索や深さ優先探索は構造がシンプルで書きやすいので、実用的です。例えば、幅優先探索のルールは、適当なスタックやキューやリスト、あるいはそれらが分からなければ大きめに確保した配列に、次に探索する頂点を格納していくことで、簡単に書くことができます。深さ優先探索のルールは、再帰関数を使えば簡単に書くことができます。
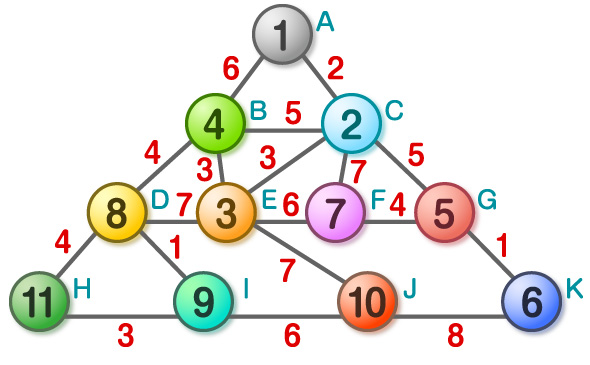
ここで、以下のようなグラフがあるとしましょう。各辺には番号が振ってありますが、この番号を、頂点間の距離とします。
このような距離が与えられているグラフでは、図のような探索順で探索することが多いです。一見すると、探索順には特定の法則がないように思えますね。幅優先探索や深さ優先探索とは違いそうです。このように探索するのは、どのようなルールが定められているからでしょうか? 考えてみてください。
気付きましたでしょうか? この探索は、「頂点Aから距離の近い順に探索している」といったルールに落とし込めますね。このような探索のことを、「最良優先探索」と呼ぶのですが、これは探索の順序を工夫したに過ぎません。頂点Aからすべての頂点への距離を列挙するのであれば、深さ優先探索や幅優先探索でも問題なく求められます。しかし、例えば「ある条件を満たす頂点のうち、最も頂点Aからの距離が短いものを探す」などといった場合には高速に求めることが可能となります。
この探索を使っているアルゴリズムで代表的なものとして、「ダイクストラ法」があります。ダイクストラ法を図にすると、以下のようなイメージになります。
この図は、先ほどの図に不要な辺を書き足しただけです。しかし、この図では、ループする個所がたくさんありますので、グラフは木構造になっていません。このまま普通に探索を試みると、無限ループに陥り、探索が終了しません。
では、このようなグラフで探索をするには、どういったルールがあればよいのでしょうか。例えば、「一度調べた頂点は、二度と調べない」というルールを追加できれば、探索できそうです。「何だ、そんな適当でいいのか」と思われるかもしれませんが、こうしたルールを思いつけるかどうかが重要です。
結局のところ、与えられる問題の形はさまざまですが、すべきことは、「問題に合った探索の方法を考える」ことだけです。移動する辺の数をできるだけ少ないものを探したいのであれば幅優先探索がよいでしょうし、すべてのパターンを列挙したいのであれば深さ優先探索が適しているでしょう。
また、先ほど挙げた、「一度探索した頂点は二度と探索しない」といったルールや、例えば「10回移動したら探索を打ち切る」といったようなルールを加えることで、不要な探索を打ち切り、計算量を大きく抑えることができます。これが「枝刈り」と呼ばれる技法です。うまいルールで枝刈りできるようになれば、初級者は脱したと考えてよいのではないでしょうか。
ただし、枝刈りは「途中で探索をやめてしまう行為」であるため、間違った枝刈りを行ってしまうと正しい答えが得られなくなってしまいます。上の例で言えば、例えば「10回移動したら探索を打ち切る」ルールを加えたとして、最適な答えが11回移動しなければ見つからないものだったなら、きちんとした答えが得られなくなってしまいます。
まとめると、探索の順序と枝刈りのルールは計算量と計算時間に大きく影響するため、問題に応じてそれらを適切に選択することがポイントです。これらの手法に対しては、さまざまな名称がつけられていたりもしますが、大切なのは、そのようなものを覚えてそれに当てはめるということではなく、自然で効率的なルールを自分で制定していく、ということになります。自然で効率的なルールが思い浮かび、かつコーディングできるようになるまでには少し慣れも必要でしょうが、それが習得できれば、コンテストではもちろん、ほかの分野でも大きく役に立つと思います。
また、探索のルールの中に不要な条件が含まれていないかを見極めることも大切です。例えば上述したダイクストラ法では、それぞれの辺が表す距離がすべて同じだとすれば、普通に幅優先探索をしていくだけで距離順に探索をすることが可能となります。そのため、ダイクストラ法で必要となる、まだ調べていない頂点の中で一番距離が短いものを探すメソッドが余計になってしまいます。冒頭で述べたように、「問題を、既存の適当なアルゴリズムに当てはめる」という考え方は、非常に危険であることがお分かりいただけるかと思います。
今回は、探索という重要な考えをじっくり理解していただきたいと思いますので、いつものような練習問題は次回にしたいと思います。まずは今回紹介した内容をしっかりと理解いただければと思います。それでは、次回もお楽しみに!
著者プロフィール:高橋直大(たかはし なおひろ)
Microsoftが主催する技術コンテスト「Imagine Cup」の2008年アルゴリズム部門で世界第3位に入賞した若きアルゴリズマー。TopCoderでは誰もが恐れるRedcoderとして活躍中。先日開催された「天下一プログラマーコンテスト」では特別賞を受賞した。現在、慶應義塾大学環境情報学部2年。口癖は「みょんみょん」。
世界でも有数のRedcoder、高橋直大がアルゴリズムの魅力と極意を伝授する「最強最速アルゴリズマー養成講座」はこちらから
関連記事
 細かすぎて伝わりにくいTopCoderのコーディングスキル向上マジック
細かすぎて伝わりにくいTopCoderのコーディングスキル向上マジック
競技プログラミングはレベルの高い人たちの集まり――そんな考えを持っている初心者の方、TopCoderはあなたのコーディングスキルを爆発的に高める魔法のような場です。今回は、初心者にこそお勧めしたいTopCoderの魅力について考えます。 「1000のアルゴリズムを持つ男」vs.「やわらか頭脳」
「1000のアルゴリズムを持つ男」vs.「やわらか頭脳」
典型的なアルゴリズムをたくさん知っている人間が最強か――? いいえ、典型的なアルゴリズムを知らなくても、違ったアプローチで答えに迫る方法はいくらでも存在します。短い実行時間で正確な答えを導き出せるかを考える習慣をつけましょう。 オーダーを極める思考法
オーダーを極める思考法
プログラムの実行に掛かる時間を把握しておくのは、プログラミングを行う上で基本的な注意点です。今回は、計算量のオーダーについて学びながら、TopCoderのMedium問題を考えてみましょう。 あなたの論理的思考とコーディング力は3倍高められる
あなたの論理的思考とコーディング力は3倍高められる
全世界で20万人を超える凄腕のコーダーが集うプログラミングコンテスト「TopCoder」。本稿では、アルゴリズム部門のSRMで取り上げられる問題を考えながら、論理的思考力およびコーディングのテクニックを養っていきます。- 高橋直大、Imagine Cupアルゴリズム部門で世界の三強に
 フランスの地でアルゴリズムの未来を切り開く男 高橋直大
フランスの地でアルゴリズムの未来を切り開く男 高橋直大
Microsoftが主催する学生向けの技術コンテスト「Imagine Cup」。そのアルゴリズム部門で世界の頂点に挑むのは、プログラミング歴が2年にも満たない一人の数学好きだった。 アルゴリズムと戯れる元野球少年が手に入れた宝物
アルゴリズムと戯れる元野球少年が手に入れた宝物
Imagine Cup 2008のアルゴリズム部門で世界第3位となった高橋直大氏。彼の軌跡を眺めてみると、わたしたちが忘れてしまったことにすら気付かない何かを思い出させてくれるような気持ちになる。 TopCoderで世界と渡り合う日本IBMの異才――夷藤勇人
TopCoderで世界と渡り合う日本IBMの異才――夷藤勇人
もしあなたが美しい(あるいはトリッキーな)コードが飛び交う世界を知りたいと願うならそれはTopCoderに参加することで容易に実現することができる。このTopCoderに参加している数少ない日本人で、生涯プログラマーを宣言する人物にTopCoderの魅力を聞いた。
関連リンク
Copyright © ITmedia, Inc. All Rights Reserved.
アイティメディアからのお知らせ
人気記事ランキング
- 知らない番号でも一瞬で正体判明? 警察庁推奨アプリの実力を検証
- AD DSにSYSTEM権限取得の脆弱性 Microsoftが修正プログラムを配布
- .NETにサービス停止の脆弱性 広範なアプリケーションに影響
- Microsoft 365の新プラン「E7」は“AI盛り盛り”で99ドル E5にはない魅力は?
- ZIPファイルの“ちょっとした細工”で検知停止 EDRも見逃す可能性
- M365版「Cowork」登場 Anthropicとの連携が生んだ「新しい仕事の進め方」
- ★4を目指すのは正解か? SCS評価制度が企業に突き付ける“本当の論点”
- 本職プログラマーから見た素人のバイブコーディングのリアル AIビジネス活用の現在地
- 偽のTeamsサポートで新型バックドアを設置 巧妙な手口に要注意
- データ激増時代に変化するIT部門の役割 データガバナンス実装の現実解