フラクタル - 自己相似形とべき乗則:オブジェクト指向の世界(29)(1/3 ページ)
前回は、慶応義塾大学SFCの「学習パターン」を紹介した。今回は話題を一転して、同じ図形パターンがスケールを変えて何度も現れるフラクタルについて考える。
前回はパターン言語事例−慶応義塾大学 湘南藤沢キャンパス(SFC)の「学習パターン」を紹介しました。個々に挙げられたパターンには普遍的なものが含まれています。
例えば、筆者は今回担当した新人研修で早速学習パターンを活用させていただきました。受講生の学校での経験の違いにより、一律に研修を行うのは講師・受講生ともに厳しいものがあります。質問も少ないです。そこで活用したのが、
(No.9)教わり上手になる
- 「ほかの人に『やってもらう』のではなく、上手に『教わる』と次につながる」
これは、講師に聞いても良いし、同期の経験者に聞いても構いません。
(No.31)教えることによる学び
- 「人に何かを教えることは、自分にとってもプラスになる」
なので、聞かれた人にもプラスになるのです。また、わずか2〜3カ月の研修ですが各自が振り返ると成長している自分に気付きます。
(No.11)成長の発見
- 「昨日の自分と今日の自分。そのわずかな違いに敏感になる」
研修終了後、現場に配属されるときにはたくましく成長しているのです。これらのパターンを折に触れ繰り返し話すことで、確かに効果が実感できました。
今回は、話題を一転してフラクタルについて考えてみたいと思います。フラクタル図形は、同じ図形パターンがスケールを変えて何度も現れます。また縮小された自己相似形の数がべき乗則で増えていきます。
なお、今回扱う「パターン」は、当連載で何度か取り上げてきたパターン言語のパターンではなく、一般的な意味でのパターンです。
フラクタルとは?
複雑な形をいくら拡大しても元の形と同じようなパターンが現れる形を、“フラクタル”と呼びます。
自然界には、植物や地形などを探せば、たくさんのフラクタル例が見つかります。植物の先端の芽から次々と同じような形をした小さな枝と葉が、無限に連なっていくように生成されていきます。このような自己相似形の無限連鎖が、フラクタルです。
例えば、アマゾンやミシシッピなどの大河の支流や、そのまた支流を拡大すると同じような川の流れのパターンが現れます。
フラクタルという概念は、元IBMフェローのブノワ・マンデルブロ氏が名付けたものです。きっかけは、シカゴ商業取引所での綿花価格の相場の変動グラフが、分単位、時間単位あるいは年単位など時間の取り方のスケールを変えても、グラフの時間軸の幅を同じにすれば同様のパターンになることを発見し、さまざまな分野について同様の現象を調査したところから始まったそうです。
フラクタルという概念の提唱者はマンデルブロ氏ですが、その人の名より、その名前を冠した図の方がよく知られているようです。図1の黒い部分をマンデルブロ集合と呼びますが、その境界辺りを拡大していくと、次々と同じようなパターンが出現します。このような不思議なパターンは、数式からは全く想定できず、コンピュータのおかげで偶然発見されたフラクタルです。
図1右のような黒い雪だるまが、サイズを変えて無数に隠れています。ちなみにこのプログラムは筆者のホームページ[*]にアップしましたので、読者の皆さまも不思議な世界にはまってください。きっと、はまります……。
【関連記事】
[*] オブジェクト指向と哲学 「フラクタル」
フラクタルの厳密な定義は決まっていないそうですが[1]、重要な特性は「1.自己相似形」と「2.べき乗則」の2点です。
Copyright © ITmedia, Inc. All Rights Reserved.
アイティメディアからのお知らせ
人気記事ランキング
- 初期侵入口は“またVPN” 日本医大武蔵小杉病院にランサムウェア攻撃
- SMBC日興証券が「パスキー」で口座乗っ取り対策 約5カ月で実現したのはなぜ?
- 生成AIの記憶機能を悪用して特定企業を優遇 50件超の事例を確認
- 日本IBMのAI戦略“3つの柱” 「制御できるAI」でレガシー資産をモダナイズ
- 「2027年1月12日」は運命の日? サポート切れOSを使い続ける会社の末路
- 人材水準を4段階で評価 「サイバー人材フレームワーク」案の意見公募を開始
- 「身近な上司」を再現する専用ディープフェイク動画を作成 KnowBe4が新トレーニング
- 富士通、ソブリンAIサーバを国内製造開始 自社開発プロセッサー搭載版も
- 「英数・記号の混在」はもう古い NISTがパスワードポリシーの要件を刷新
- 「AI前提」の国家戦略と「思考停止」の現場 大半の企業で“何も起きない”未来を予見
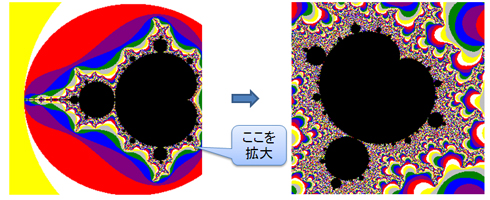 図1. マンデルブロ集合
図1. マンデルブロ集合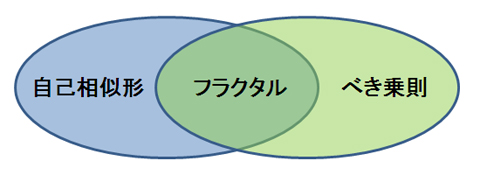 図2. フラクタルの定義
図2. フラクタルの定義