50年以上の未解決問題「ソファ移動問題」を数学的に解決か 韓国の研究者が発表 L字の廊下を曲がれる最大の大きさとは：Innovative Tech

[山下裕毅，ITmedia]

Innovative Tech：

このコーナーでは、2014年から先端テクノロジーの研究を論文単位で記事にしているWebメディア「Seamless」（シームレス）を主宰する山下裕毅氏が執筆。新規性の高い科学論文を山下氏がピックアップし、解説する。

X： ＠shiropen2

　韓国の延世大学に所属するペク・チネさんが発表した論文「Optimality of Gerver’s Sofa」は、1966年からの未解決問題「ソファ移動問題」（Moving sofa problem）を解決したという研究報告である。

L字の廊下をソファを運んで曲がる問題

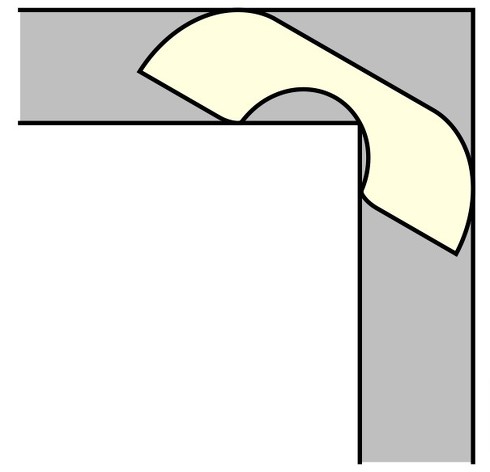
　この問題は、家具を引っ越す際、大きなソファを例えば、幅1mの廊下の直角の曲がり角で運ぶことを考える。このとき、廊下を曲がることのできる最大の面積を持つソファ（平面図形）はどのようなものか、という問題である。

　数学的には次のように定式化できる。幅1の直角の廊下があり、水平な通路から垂直な通路へとつながっている。この廊下の中を連続的に動かせる平面図形の中で、最大の面積を持つものを求める。ただし図形は途中で切断したり変形したりはできない。

　1992年に作家のジョセフ・ガーバーさんは、面積約2.2195……の特殊な形状（ガーバーのソファ）を考案。この図形は、まるでL字型の廊下に合わせて「へこみ」を持つような形をしている。この「へこみ」により、図形は廊下を効率的に曲がることができる。

ガーバーのソファはL字型の廊下を効率的に曲がることが可能

L字型の廊下を通過するガーバーのソファ

　今回発表した論文では、このガーバーのソファが実際に最大面積を持つことを証明した。証明は3つのステップからなる。

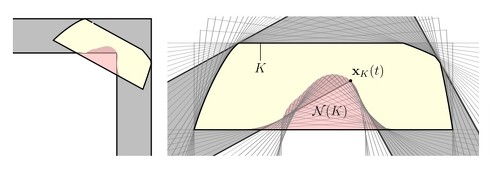
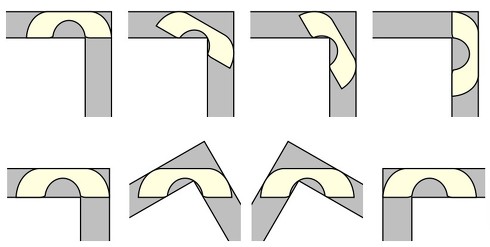
　最初に、この最大のソファは単調な形をしており、真っすぐな辺を持つ凸形状から、L字型の廊下の内側の角に合わせて一部が削られた形となっている。このソファは動く際に、辺の長さが互いにバランスよく保たれている。また、移動中に90度の角度を完全に回転することも証明された。

　次のステップでは、図形が満たすべき「単射条件」という性質を導く。これは、L字型廊下の内側の角が描く軌跡を、動いているソファから見たとき、その軌跡は交差することがないというもの。この性質は、最後のステップで図形の面積を評価する際に重要となる。

　最後のステップでは、単射条件を満たす図形の面積の上限値を求める。これは図形を3つの凸集合の組み合わせとして表現することで行われる。「マミコンの定理」という図形の面積に関する定理を使って、この上限値が「凹性」という数学的な性質を持つことを証明する。

　さらに、2018年にロミックが発見した方程式を使って、この上限値の変化率（方向微分）を調べ、ガーバーのソファの形状が局所的な最大値となることを示す。

　上限値の凹性という性質により、この局所的な最大値は大域的な最大値でもあることが分かる。これによって、ガーバーのソファが可能な限り最大の面積を持つことが証明されたとしている。

Source and Image Credits: Baek, Jineon. “Optimality of Gerver’s Sofa.” arXiv preprint arXiv:2411.19826（2024）.