日本の会社員が発見、数学界を賑わせた「新図形」とは？ 論文も5日間で執筆、arXivにも掲載：Innovative Tech（2/2 ページ）

[山下裕毅，ITmedia]

ステップ1：「余りの数列」で折れ線を描く

　このタイリングの出発点は、「割り算の余り」を使う。例えば「3の倍数を7で割った余り」を順番に計算してみよう。

3×0＝0 → 7で割った余りは 0

3×1＝3 → 7で割った余りは 3

3×2＝6 → 7で割った余りは 6

3×3＝9 → 7で割った余りは 2

3×4＝12 → 7で割った余りは 5

3×5＝15 → 7で割った余りは 1

3×6＝18 → 7で割った余りは 4

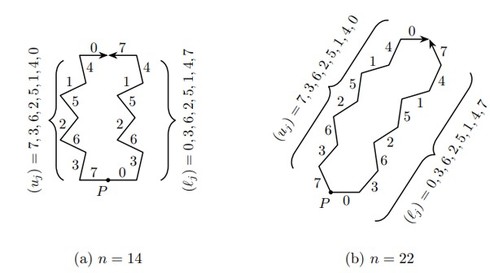
　こうして「0, 3, 6, 2, 5, 1, 4」という数列が得られる。0〜6までの数字がちょうど1回ずつ、バラバラの順番で現れているのが面白い。さらに、数字の入れ替えをするため（ステップ2で説明）、数列の最後に7を加えて「0, 3, 6, 2, 5, 1, 4, 7」という数列を用意する。

　次に、円周上に等間隔で方向を設定する（時計の文字盤のようなイメージ）。そして、数列の各数字を「次にどの方向へ1歩進むか」という指示だと解釈して、折れ線を描いていく。「0」なら0番の方向へ、「3」なら3番の方向へという具合だ。こうしてできる折れ線は、規則的なようでいて不規則な、独特のギザギザ模様になる。

ステップ2：折れ線から「基本タイル」をつくる

　ステップ1の数列（「0, 3, 6, 2, 5, 1, 4, 7」）の最初と最後の数字（この例では0, 7）を入れ替えた数列（「7, 3, 6, 2, 5, 1, 4, 0」）を用意する。この2つの数列から、同じ出発点で2本の折れ線を描くと、どちらも同じ終点にたどり着く。2本の折れ線で囲まれた領域が、このタイリングの「基本タイル」になる。稲妻のような、左右非対称の細長い多角形だ。

余りの数列から作られる2本の折れ線（下側の経路と上側の経路）で囲まれた基本タイルの例（論文から引用）

基本タイル（「普通の会社員が新しい図形を発見したのでハンガリーのポスドクの助けを借りてarXivに論文を投稿した話」から引用）

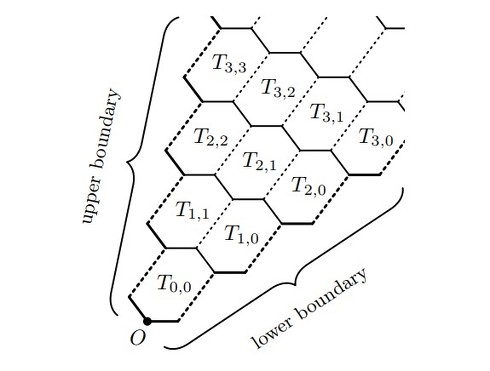
ステップ3：基本タイルで「扇形の領域」を埋める

　この基本タイルを、向きを変えずに規則正しく並べていくと、中心から広がる扇形の領域を隙間なく敷き詰めることができる。重要なのは、この扇形の中では、タイルの並び方は規則的なパターンに従っているという点だ。

基本タイルを規則正しく並べて扇形を敷き詰めた様子（論文から引用）

ステップ4：扇形を組み合わせて平面全体を埋める

　最後に、この扇形を中心のまわりで少しずつ回転させながら、何枚も並べていく。このとき、扇形のギザギザの境界線が、隣り合う扇形どうしでぴったりとかみ合うようになっているのだ。こうして平面全体が埋め尽くされるのだが、完成したパターンを見渡すと、全体としては同じ配置の繰り返しがどこにもない。つまり非周期的なパターンになっているのだ。

　この仕組みの面白いところは、最初に選ぶ2つの数字（上の例では3と7）を変えるだけで、まったく違う模様が生まれること。（3, 7）を選べば稲妻のような模様、（2, 5）を選べば別の模様、（7, 17）ならさらに複雑な模様というように、組み合わせの数だけ異なるパターンを作り出せる。さらに「折れ線が曲がれる角度の細かさ」を調整することで、同じ数字の組み合わせからも異なる形のタイルを作り出せる。

パラメータを変えることで生成されるさまざまなModulo Krinkle tilingのパターン例（論文から引用）

2023年の大発見とは別物、でも身近なのがいい

　ここで誤解のないように説明しておきたいのは、Modulo Krinkle tilingは2023年に発見された「Hat」や「Spectre」とは性質が異なるということだ。

　HatやSpectreは、その形を使うと、どう頑張っても非周期的にしか敷き詰められないという特別な図形だった。一方、Modulo Krinkle tilingの基本タイルは、扇形の中では周期的に並んでいる。つまり、やろうと思えば周期的なパターンも作れる。

　Modulo Krinkle tilingは、長年の未解決問題を解決したわけではない。しかし、「割り算の余り」という身近な計算から、誰も見たことのない美しいパターンが無数に生み出せることを示した。

　論文の著者であるImura氏は、今後も数学とアートの境界領域での活動を続けていくという。プロジェクトページも立ち上げており、そこではパラメータを操作してModulo Krinkle tilingをリアルタイムに生成するデモや、タイルパターンを用いたグッズの販売をおこなっている。また国際会議への参加も視野に入れているそうだ。

　趣味で始めた幾何学パターンの探求が、世界中の人々の関心を集め、論文として形になった。この過程は、数学が決して専門家だけのものではないことを教えてくれる。好奇心を持って考え続ければ、誰でも新しい発見に出会える可能性がある。Modulo Krinkle tilingは、そんな希望を感じさせてくれる発見といえるだろう。