　玉川大学と千葉大学に所属する川崎敏治さん（崎はたつさき）の単著論文「A proof of the Collatz conjecture」がarXivでプレプリント（査読前）として登場した。新たな不動点定理を使用して、数学の未解決問題「コラッツ予想」を証明したという。査読前のため現時点で真偽はまだだが、全世界の数学者たちがその真偽を確かめるだろう。

arXivに投稿された論文のアブストラクト

　コラッツ予想とは、整数論における未解決問題の一つであり、1937年にドイツの数学者ローター・コラッツが提唱した。コラッツ予想では以下の操作を考える。

任意の正の整数nから始め、nが偶数ならば2で割り、奇数ならば3倍して1を加える。この操作を得られた数に対して繰り返す。

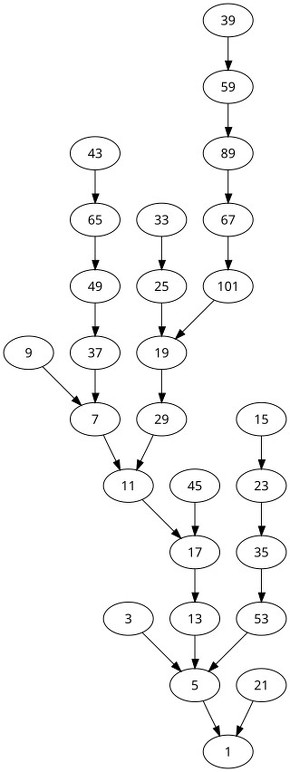
　コラッツ予想は、どのような正の整数から始めても、この操作を繰り返すと最終的には必ず1に到達するというものである。例えばn=10の場合は、10→5→16→8→4→2→1、と続いて1にたどり着く。

　このように複雑な経路をたどりながらも最終的には1に収束するという性質だが、これが全ての正の整数に対して成り立つことは数学的に証明されていない。

50未満の正の整数の軌道を示したグラフ（27、31、41、47はのぞく）（Wikipediaから引用）

　20世紀の偉大な数学者の一人であるポール・エルデシュ氏や、2006年にフィールズ賞を受賞した米UCLAのテレンス・タオ教授、米ミシガン大学のジェフリー・ラガリアス教授など、数多くの数学者がコラッツ予想の難しさについて述べている。特にラガリアス教授は「現在の数学では全く手の届かないものだ」と自身の書籍で言及している。

　今回のプレプリントの発表によって、SNS上でも一部ユーザーたちの間で話題になっている。中には内容を読み検証したと思われるユーザーもおり「一部主張が成り立たないのでは」という主張も見られる。

Source and Image Credits: Kawasaki, Toshiharu. “A Proof of the Collatz Conjecture.” arXiv preprint arXiv:2502.2064（2025）.

NTT、計算機科学の未解決問題を解決　著名教科書の「二分決定グラフ」に関する誤りを指摘
NTTは、数学の未解決問題を解決したと発表した。同社が解決したのは、著名なデータ構造として知られる「二分決定グラフ」に関する未解決問題だ。
“N/S高研究部の学生2人”が数学の未解決問題を解決か　プレプリントで論文公開
N/S高研究部（KdEi研）に所属する横井杏樹さん（高1）と、N/S高研究部アドバイザーで東京理科大学に所属する川村花道さんは、数学の「多重ゼータ値」に関する未解決問題を解決したという研究報告を発表した。
50年以上の未解決問題「ソファ移動問題」を数学的に解決か　韓国の研究者が発表　L字の廊下を曲がれる最大の大きさとは
韓国の延世大学に所属するペク・チネさんは、1966年からの未解決問題「ソファ移動問題」（Moving sofa problem）を解決したという研究報告を発表した。
米国の女子高校生2人「ピタゴラスの定理」を新証明　しかも5通り　査読済みで権威ある学術誌に登場
2023年、米国の高校生ネキヤ・ジャクソンさんとカルセア・ジョンソンさんは、地元の高校のコンテストで驚くべき成果を披露した。それは、三角関数を用いてピタゴラスの定理を証明するという方法の発見であった。
“セガ流”数学の学び方とは？　書籍「セガ的基礎線形代数講座」発売へ　ゲーム開発に必要な知識を収録
日本評論社は、セガが社内勉強会で使う数学テキストを書籍化した「セガ的基礎線形代数講座」を発売する。