試してびっくり 点を回転させると円に見える「グラス・パターン」錯視の謎:コンピュータで“錯視”の謎に迫る
今回は「グラス・パターン」という図形について紹介したいと思います。まずはドットをランダムに散らした透明なシートを1枚用意します(下図参照)。
この画像を「ランダムドットA」と呼ぶことにしましょう。さらにランダムドットAと全く同じ透明シートをもう1枚用意し、そのコピーを元のシート(ランダムドットA)の上にぴったりと重ねます。次に、中心を軸にして上に載せたコピーのシートだけを反時計回り、あるいは時計回りに少し回転させます。ここでは反時計回りに回してみました。すると次のように図が変化します。
ドットが一斉に同心円状の形に並んだように見えませんか? ランダムドットAのドットが回転方向へ規則的にずれて配置されるとはいえ、ランダムに配置されたドットたちが、きれいに同心円状として見えるのはなぜでしょう。
この現象は1969年にレオン・グラスという人物により発見され、グラス・パターンと呼ばれています。今回の主役はこのグラス・パターンです。
連載:コンピュータで“錯視”の謎に迫る
あなたが今見ているものは、脳がだまされて見えているだけかも……。この連載では、数学やコンピュータの技術を使って目に錯覚を起こしたり、錯覚を取り除いたり──。テクノロジーでひもとく不思議な「錯視」の世界をご紹介します。
“ランダム”が重要!
ここでクイズです。同じ条件で、ランダムではなく規則正しく並んだ点の場合はどうなるでしょうか。例えば下の図3のように、格子状にきれいに並んだ点をプリントした透明なシートを用意します。
これと全く同じものをもう1枚作り、グラス・パターンのときと同じくシートを重ねて上側のシートだけを反時計回りに回します。するとどんな図形が現れるでしょうか。
答えは次の画像の通りです。ドットが同心円状に並んでいるようには見えず、むしろ小さな同心円のグループが格子状に並んでいるように見えます。この現象もすでに知られているものです。
グラス・パターンはなぜ同心円に見えるのか?
筆者がグラス・パターンに惹かれたのは14年。この年の10月に東京大学の幾何(きか)学者、坪井俊教授からグラス・パターンの画像を添付した電子メールが送られてきて、「なぜこれが同心円に見えるのか数学を使って説明できないか」という趣旨のご質問を頂きました。即座に思い付いたのは、次のようなことです。
「以前、筆者らは『幾何的フィルター』を作り、『フラクタル螺旋錯視』の錯視成分を特定、錯視の除去を行った。この方法が使えるのではないか」(Arai and Arai 【1】、本連載第2回も参照)
幾何的フィルターというのは、同心円や渦巻きなどに強く反応するように作ったデジタルフィルターのようなものです。93年と96年にギャラントらがマカクザルを使った実験で、脳の「V4野」というところに同心円や渦巻きなどに強く反応する神経細胞があると報告しています。幾何的フィルターはそのような神経細胞による視覚情報の処理を数式で表しているのではないかと考えています。
早速、筆者と共同研究者の新井しのぶは、幾何的フィルターを用いてグラス・パターンの解析を行い、結果を坪井教授に返信しました。この記事では、そのときに考案した方法でランダムドットAから作ったグラス・パターンを解析してみることにします。
グラス・パターンが同心円に見える成分を除去
一口に同心円、あるいは渦巻きに反応する幾何的フィルターといっても、その種類はたくさんあります。それらは画像が入力されると、その画像をいろいろな成分に分解します。この幾何的フィルターたちによって、ランダムドットAから作られるグラス・パターンの画像を分解したところ、同心円の検出に寄与しない幾何的フィルターと、寄与すると考えられるものがありました。下の図をご覧ください。
(A)は解析する前のグラス・パターンです。スペースの節約のため四半分のみ載せています。幾何的フィルターたちを(A)の同心円検出に関与すると考えられるものと、そうでないものに分けます。前者の幾何的フィルターにより抽出されたデータを全部合わせたものが (B)です。(C)はそうではない幾何的フィルターによるデータを合わせたものです。(B) には同心円が認められますが、(C)には同心円が認められません。
ここで
(A)=(B)+(C)
となっています。つまりグラス・パターンは、同心円が認められる成分と、そうでないものとに二分されています。これによりグラス・パターンが同心円に見えることに寄与する幾何的フィルターたちを絞り込むことができたわけです。
この解析からランダムドットAから作ったグラス・パターンについては、同心円を検出する幾何的フィルタのほかに、“同心円に近い渦巻き”に強く反応するものもグラス・パターンの検出に関与していることが分かりました。
なお、ここでの解析はランダムドットAから作ったグラス・パターンに関するもので、ドットの大きさやドットの数を大幅に変えると、関連する幾何的フィルターも変わってきます。
これまでのグラス・パターンの視覚科学的な研究
この記事では紹介しませんでしたが、同心円以外の形状、例えば渦巻き、放射線、双曲線などが見えるグラス・パターンも知られています(グラス、ペレツ、1973年)。
こういったグラス・パターンが発見されてから、その発生を脳内の神経細胞による視覚情報処理のメカニズムから説明しようとする研究がたくさん行われてきました。特にV4野の神経細胞については、93年、96年にギャラントら、そして94年に小畠、田中により研究が進み、その成果を踏まえて97年と98年にウィルソンとウィルキンソンらが、V4野の神経細胞とグラス・パターンとの関連を示す論文を発表しています。
その他、北岡・ピンナ・ブレルスタッフ (2001)でも論じられています。11年までのグラス・パターンの研究にどのようなものがあるのかは、グラス自身らによるScholarpedia【2】に大方まとめられています。興味のある方はご覧いただくとよいでしょう。(なお、【2】によりますと、“グラス・パターン”という命名は、視覚の計算理論で有名なデビッド・マー (1982)によるそうです)
本記事では、坪井教授からの質問を出発点として行ったグラス・パターンに関する筆者と新井しのぶによる数学的な解析結果の一部を紹介しました。しかし、まだ解決に至ったというわけではありません。脳内で行われている視覚の情報処理を数式で表す数理モデルの研究にとって、グラス・パターンは非常に興味深い問題であると思います。
「ランダム」とは何か、は数学上の難しい問題ですのでここでは立ち入りません。ランダムドットAはMATLABで乱数を作る機能 rand を使っています。
- 引用文献
【1】 H. Arai and S. Arai, Framelet analysis of some geometrical illusions, Japan J. Indust. Appl. Math. 27 (2010), pp. 23-46.
【2】 Leon Glass and Matthew A. Smith (2011), Glass patterns, Scholarpedia, 6 (8):9594.
http://www.scholarpedia.org/article/Glass_patterns
著者:新井仁之(あらい ひとし)
東京大学大学院数理科学研究科・教授、理学博士。
横浜市生まれ。早稲田大学、東北大学を経て現職。
視覚と錯視の数学的新理論の研究により、平成20年度科学技術分野の文部科学大臣表彰科学技術賞(研究部門)を受賞、また1997年に複素解析と調和解析の研究で日本数学会賞春季賞を受賞。
ITmedia NEWSの錯覚関連記事
あなたはどう見える? 「静止画が動いて見える」不思議な錯視の世界
「あなたは何色に見える?」──“ドレスの色”問題が再来 今度は「サンダル」
「白と金」「いや青と黒だ」あなたはどっちに見える? 1枚の写真をめぐりネットで激論
関連記事
 真っすぐなのに斜めに見える“不思議な文字列” その仕組みとは?
真っすぐなのに斜めに見える“不思議な文字列” その仕組みとは?
東大・新井仁之教授が解説する錯視の世界。第6回では、平行なのに文字が傾いて見える「文字列傾斜錯視」の謎に迫ります。文字列が傾斜する錯視文字列の自動生成ソフトも期間限定で公開! 2つ並んだ正方形、あなたは同じ色に見える? 「客のクレーム対応」で始まった錯視研究とは
2つ並んだ正方形、あなたは同じ色に見える? 「客のクレーム対応」で始まった錯視研究とは
東大・新井仁之教授が解説する錯視の世界。同じ色が違って見える「色の同時対比」という錯視を紹介する。 「トランプマークが浮いて見える」不思議な画像 どうやって作っている?
「トランプマークが浮いて見える」不思議な画像 どうやって作っている?
東大・新井仁之教授が解説する錯視の世界。今回は「錯視画像を作る技術」を紹介する。 あなたはどう見える? 「静止画が動いて見える」不思議な錯視の世界
あなたはどう見える? 「静止画が動いて見える」不思議な錯視の世界
東大の新井仁之教授が解説する錯視連載が本格スタート。「オオウチ錯視」「ピンナ錯視」って知ってます? 錯視画像から「数学」で“錯視”を取りのぞけるってホント?
錯視画像から「数学」で“錯視”を取りのぞけるってホント?
あなたはどう見える? 錯視画像から錯視要素を取りのぞいたり強めたりできるとな。 指でなぞるとびっくり! 驚きの“渦巻き錯視”って知ってる?
指でなぞるとびっくり! 驚きの“渦巻き錯視”って知ってる?
ぐるぐる渦巻いているように見えるけど、実は渦巻きじゃなくて円が重なっているだけ……!?
関連リンク
Copyright © ITmedia, Inc. All Rights Reserved.
Special
PR

 ランダムドットAを重ねて回転させると……(
ランダムドットAを重ねて回転させると……(

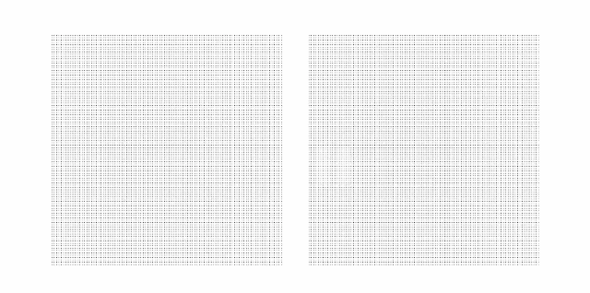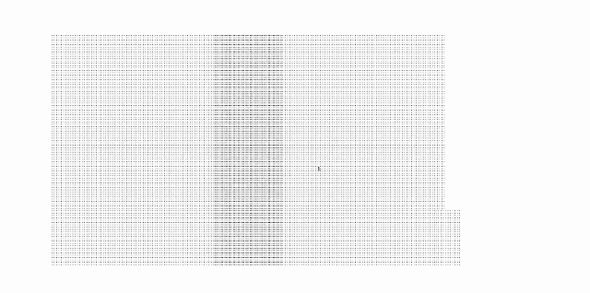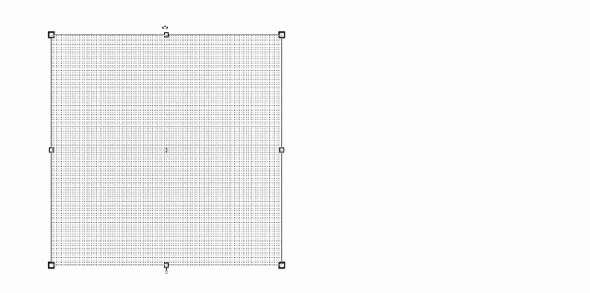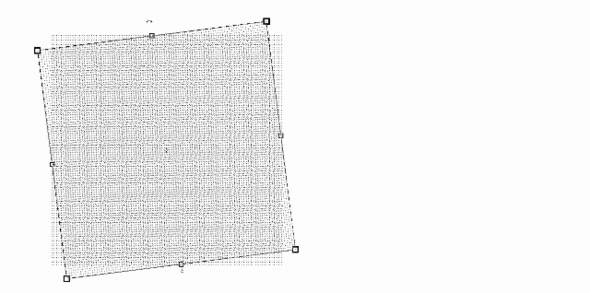 格子状のドットを重ねて回転させると……(
格子状のドットを重ねて回転させると……(





