「視力300万」は視力検査でどれくらい見える？　ブラックホール観測の“超高精度”を数字で味わう

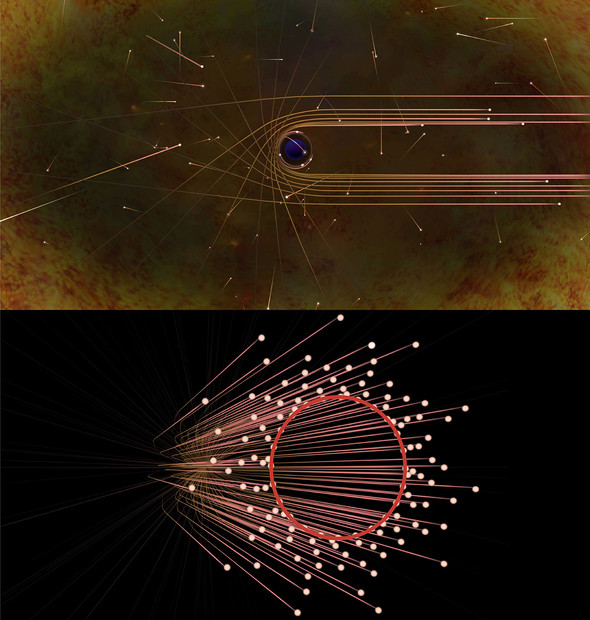
　国立天文台が参加する国際プロジェクト「イベント・ホライズン・テレスコープ」は4月10日、初めてブラックホールの影の観測に成功したと発表した。

　観測したブラックホールはおとめ座銀河団の楕円銀河M87の中心に位置する巨大ブラックホール。地球から約5500万光年の彼方（かなた）にあり、質量は太陽の約65億倍だという。

　ブラックホールの影の直径は約1000億キロメートルで、ブラックホールの表面といえる「事象の地平面」（イベント・ホライズン）の直径は約400億キロメートル。非常に大きな数字だが、地球から見たときの角度はわずか約42マイクロ秒角（＝約1.2度の1億分の1）。

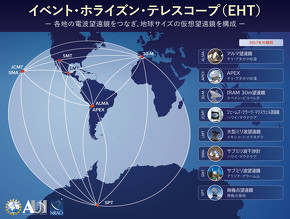
　今回観測に用いた仕組みは、「超長基線電波干渉計」（VLBI）という、世界各地の望遠鏡を束ねて仮想的に地球サイズの望遠鏡を構成するもの。チリ、スペイン、ハワイ、メキシコ、アリゾナ、南極にある計8つの電波望遠鏡を同期させることで、20マイクロ秒角の解像度を実現した。

　国立天文台は、20マイクロ秒角を「人間の視力300万に相当」「月面に置いたゴルフボールが見えるほど」と説明する。

　月面のゴルフボールが見えるという説明でも十分そのすごさは伝わってくるが、せっかく「視力300万」という例えもあるので、「視力300万なら視力検査でどれくらい小さいものが見えるのか」ということも計算してみたい。

　なお、この計算はVLBIで近くのものが見えるということを示しているわけではなく、あくまで例えであることを先に断っておく。

5メートル先の視力検査を視力300万で見てみると

　視力1.0とは、1分角（60分の1度）を識別できることであり、5メートル先のランドルト環（「C」のマーク）の切れ目約1.45ミリメートルを認識できることに等しい。

　これは三角比の、

tan(角度) ×（底辺の長さ）＝（対辺の長さ）

　という関係式に値を代入することでも確認できる。

　では、20マイクロ秒角で5メートル先を見るとどれほど小さいものが見えるのか、式から計算してみよう。

　視角の計算の場合、鋭角θの直角三角形ではなく、鋭角θ/2の直角三角形が上下に対称となった二等辺三角形と見て計算するべきなので、

tan(10マイクロ秒角) × 5メートル × 2 ＝ 約5 × 10^(-10)メートル

　と計算できる。

　5×10のマイナス10乗メートルはすなわち0.5ナノメートルだ。PM2.5と呼ばれる微粒子の大きさが2.5マイクロメートル（以下）で、1ナノメートルの2500倍に当たる。水素原子の直径が約0.1ナノメートルなので、視力300万は5メートル先に水素原子が5つ並んでいるところを認識できるはずだ。

　まとめると、「視力300万は視力検査で水素原子5つ分の隙間を識別できる」といえる。

　もちろん、電波望遠鏡は顕微鏡ではなく、これほど近くに焦点を合わせられるものでもない。

　しかしブラックホールの観測に必要な精度がどれほどのものか、この例えからでも感じられるのではないだろうか。

　他にも実験の詳細を見ていると、各望遠鏡に正確な時を刻む原子時計を設置して正確な同期を測ったり、500テラバイトの観測データの合成・解析・確認を2年かけて行ったりと、精度を確保するための慎重さが見て取れる。

　世界の天文学者が力を合わせた超高精度の偉業が、今回のブラックホール観測につながったといえる。

この記事の著者

関連記事

• 

  はやぶさ2、人工クレーター作る実験に成功　「宇宙探査の新しい手段を確立」

• 

  写真で見る「はやぶさ2」の旅路