目の錯覚、誰がどうやって見つける? 学術研究で理論的に発見された錯視:コンピュータで“錯視”の謎に迫る(2/3 ページ)
直線から円へ
先行研究の話から始めましょう。発端は1908年にまでさかのぼります。この年、イギリスの心理学者であるジェームズ・フレーザー氏は、自身が発見した錯視をいくつか発表しました(補注2)。今回の話に関連するのはそのうちの2つです。その1つは次の図のような平行に配置されたねじれ紐が傾いて見える錯視です。
もう一つは下の図で、連載第1回でも紹介したフレーザーの渦巻き錯視です。この錯視は、ねじれ紐から作った円をいくつも同心円に並べているのに、渦巻いて見えるというものです。
さて、時間は飛んで2001年になります。心理学者の北岡明佳氏ら([KPB])は、ねじれ紐に限らず傾き錯視を起こすパターンを円にして同心円状に並べれば、渦巻き錯視ができることを発見し、数多くの例を発表しました。北岡氏らはこの現象の原因が恐らく渦巻きパターンの検出機能の誤作動にあるとし(補注3)、その検出機能があることの証拠の例として、ギャラントらが発見した渦巻きパターンに反応する脳内の神経細胞をあげました。
【補注3】「Perhaps, then, the spiral effect is a consequence of a mechanism that fires a unitary spiral detector – in our case erroneously.」([KPB]より引用)
脳のV4野へ
ここでギャラントらの発見について触れておきましょう。彼らは動物実験でマカクザルの大脳皮質のV4野という場所に、渦巻きパターンに反応する神経細胞があることを発見しました([G1]、[G2])。V4野は視覚情報を処理する脳の領野でも、比較的深いところに位置しています。ここで言う「深い」とは、初期視覚野よりも後に処理されるという意味です。V4野では視知覚のうち、形の分析や色の恒常性に関する処理などが行われているとされています([C]参照)。
ところでギャラントらが発見したのは、渦巻きパターンに反応する神経細胞だけではありません。彼らはその他にも、図3(A)に挙げた直角双曲線座標のパターンや、それの原点を中心に少しずつ回転させたようなパターンなどに反応する神経細胞も報告しています。
とすれば、「傾きの錯視を直角双曲線座標のように配列すれば、原点を中心に少し回転したように見える錯視が起こるはずだ」
私は共同研究者の新井しのぶとそのように推測しました。実際にフレーザーのねじれ紐を使って確かめたのが図1の双曲型錯視です。
このように私たちは、心理学者や神経科学者たちの研究成果の積み重ねの上に乗って、ねじれ紐の双曲型錯視を考えるに至りました。
カメの錯視を使ったら、もっと面白いかも
ところで、フレーザーのねじれ紐で予想通りの錯視効果を確認した私たちは、さらに北岡明佳氏らの論文([KPB])で発表されたカメの錯視(論文[K]によれば、正式名称は「縁飾りエッジの錯視」)に着目しました。カメの錯視は次のユニットから構成されます。
北岡氏らの論文[KPB]では、カメの錯視のユニットを同心円状に並べたものが渦巻き錯視になることが示されています。さらに北岡氏はこの他にもカメの錯視のユニットを使ったさまざまな錯視を作成しています([K]参照)。
私たちがカメの錯視のユニットに着目した理由は、単純に「縦と横に並べると縦方向にも横方向にも傾いて見える」というこの錯視の特性にありました。
カメの錯視の特性と、直角双曲線座標の数学的な性質から、私と新井しのぶは次のように推測しました。
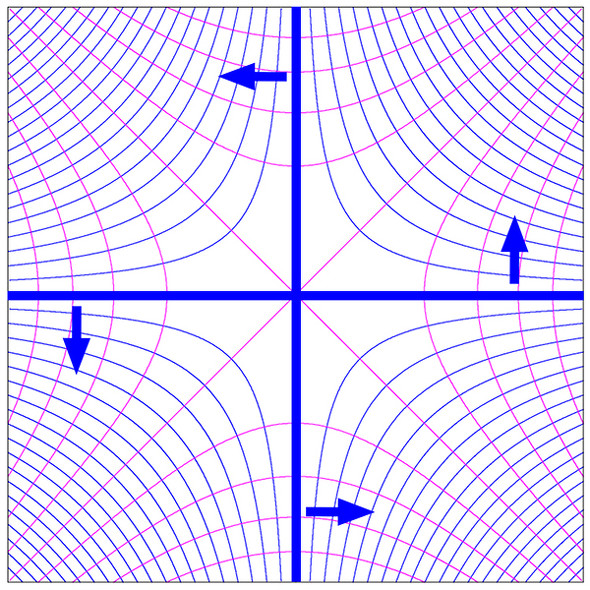
「もしカメの錯視から双曲型錯視を作れば、それは直角双曲線座標の赤色の座標軸(下図参照)に対してだけでなく、赤色の曲線と直交した青色の座標軸に対しても、ずれて見える錯視が起こるであろう。(補注4参照)」
結果は予測通り次のようになりました。
カメの錯視を用いた双曲型錯視では、ねじれ紐を用いた双曲型錯視と違い、対角方向だけでなく垂直・水平方向の軸とのずれも知覚できます。
【補注4】 ある平面領域からある平面領域への写像で、角度を保存する(正確には角度を保存し、正則性のある)ものを数学では等角写像と言います(例えば[A2]参照)。等角写像と傾きの錯視に関しては、例えばデカルト座標から極座標、直角双曲線座標以外にも楕円座標への変換(いずれも特定の点を除いて等角性がある)でも錯視が起こる例を確認しています。等角性と錯視については[A1]参照。
Copyright © ITmedia, Inc. All Rights Reserved.
Special
PR