ジグソーパズルを解くのに“数学的に完璧”な机の大きさは? カナダの研究チームが解明:Innovative Tech
Innovative Tech:
このコーナーでは、2014年から先端テクノロジーの研究を論文単位で記事にしているWebメディア「Seamless」(シームレス)を主宰する山下裕毅氏が執筆。新規性の高い科学論文を山下氏がピックアップし、解説する。
Twitter: @shiropen2
カナダのトロント大学とNational Research Council Canadaに所属する研究者らが発表した論文「How big a table do you need for your jigsaw puzzle?」は、ジグソーパズルを解くのに最適なテーブルのサイズを数学的に解明した研究報告である。
この研究では、ジグソーパズルを行う際に、最適なテーブルサイズを選ぶ方法として、完成したパズルの面積を約1.73倍することを提案。これにより、全てのピースを重ならずに平らに並べるのに十分なスペースが確保される。
研究者らは、組み立てられる前の全てのピースが正方形の表面積を占めるという前提で、各正方形がその角を触れる円の中にあると仮定した。そして、この複数の円が重なることなく2次元の表面上に最適に敷き詰められる可能な形として、六角形のパターンで並べると、ピースが重なることなくかみ合うことをみいだした。各六角形の中には、1つの完全な円と6つの円の一部が含まれる。
研究者らは、六角形のパターンに並べられた組み立て前のパズルピースが占める面積は、常に完成したパズルの総面積(長さと幅を乗じたもの)に√3、すなわち約1.73を乗じたものになることを発見した。
この法則は長方形の形状をしたジグソーパズルピースにも適用可能で、これらも同様に円の中に収まる。また、ピースのサイズや数が変わっても同様の結果が得られる。例えば、ピース間の隙間(六角形の格子の間隔)は、ピースが小さくなれば小さくなるが、ピースの数が多くなる分、隙間も多くなる。
実用性を検証するために、333平方cm(9ピース)から6798平方cm(2000ピース)までの範囲の9つのパズルについて組み立て前と組み立てた状態の面積を測定し、理論的な予測と実際の測定結果が一致することを示した。
Source and Image Credits: Bonsma-Fisher, M., & Bonsma-Fisher, K.(2023). How big a table do you need for your jigsaw puzzle?. arXiv preprint arXiv:2312.04588.
関連記事
 数学の未解決問題「アインシュタイン問題」が解決? 1つの図形だけで敷き詰めても“周期性が生まれない”
数学の未解決問題「アインシュタイン問題」が解決? 1つの図形だけで敷き詰めても“周期性が生まれない”
英国の数学者らと、カナダのウォータールー大学と米アーカンソー大学に所属する研究者らは、繰り返しパターンを作らず、2次元の表面を無限に敷き詰めることができる単一のタイル形状を発見した研究報告を発表した。 数学の未解決問題「アインシュタイン問題」を“完全解決”する新図形発見 「The hat」を改良
数学の未解決問題「アインシュタイン問題」を“完全解決”する新図形発見 「The hat」を改良
英国の数学者ら、カナダのウォータールー大学と米National Museum of Mathematicsに所属する研究者らは、繰り返しパターンを作らず、鏡像なしで、2次元の表面を無限に敷き詰めることができる単一の非周期タイルを発見した研究報告を発表した。 “ABC予想証明”の欠陥発見に賞金1.4億円 ドワンゴ創業者の川上さんが設置
“ABC予想証明”の欠陥発見に賞金1.4億円 ドワンゴ創業者の川上さんが設置
数学の未解決問題「ABC予想」を証明する理論の欠陥を指摘できれば賞金1.4億円──一般社団法人日本財団ドワンゴ学園準備会は、そんな取り組みを始めると発表した。 人だと正解率92%なのに、GPT-4だと15%になる新型テスト集「GAIA」 米Metaなどが開発
人だと正解率92%なのに、GPT-4だと15%になる新型テスト集「GAIA」 米Metaなどが開発
米Metaや米HuggingFaceなどに所属する研究者らは、難しいタスクではなく、人間にとって簡単なタスクを達成する大規模言語モデル(LLM)を評価するためのベンチマークを発表した。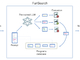 Google DeepMind、LLM採用AIシステム「FunSearch」で数学的難問を解決
Google DeepMind、LLM採用AIシステム「FunSearch」で数学的難問を解決
Google DeepMindは、LLM採用のAIシステム「FunSearch」を発表した。LLMとLLMによる幻覚を防止する“評価器”を組み合わせたもので、「ビンパッキング問題」向けの実用的なアルゴリズムも出力できる。
関連リンク
Copyright © ITmedia, Inc. All Rights Reserved.
Special
PR



