素人でもディープラーニングができる「NVIDIA DIGITS」で文字認識をやってみた（1/2 ページ）

[井上輝一，ITmedia]

　素人でもディープラーニングが使えるようになる講座がある。そんな案内がNVIDIAから届いた。

　ディープラーニングといえば、2016年に囲碁でイ・セドルに勝利した「Alpha Go」や、自動車の自動運転技術に採用されているアルゴリズムだ。

　一般的に、ディープラーニングを自分でいじってみようと思うとPythonなどプログラミング言語の理解や、GPUの用意などハードウェア的な面である程度のハードルがある。

　そういったハードルの高さから「ディープラーニングってよく聞くけれどどんなものなのだろう」と興味を持っても、説明を読む程度で実際に使用するところまでたどり着かない人も多いだろう。

　かく言う私も、プログラミングはJavaの経験が少々あるもののPythonは触ったことがなく、ディープラーニングについては概念図を見てなんとなく理解した気になっていた程度だった。

　そんな中届いた「NVIDIA Deep Learning Institute 2017」の案内を読むと、

• ディープラーニングをこれから始める方を対象に、必要な基本知識について説明
• ディープ ニューラル ネットワークを用いた画像分類を実現するためのワークフローを体験。事前知識はWebブラウザの操作ができること

　といったことが書いてある。なんと、プログラミングの知識がなくてもディープラーニングを体験できるという。

　「素人でも始められるディープラーニング」の講座をNVIDIA Deep Learning Institute 2017で受講してきたので、その内容を紹介しよう。ただ、聞いた内容を忠実に書いたつもりだが私自身もディープラーニングの素人であるから、幾分か表現が厳密ではないところもあるかもしれないのでそこはご容赦いただきたい。

使うツールは「NVIDIA DIGITS」　しかも学習用環境がクラウド上に

　今回使用するのは「NVIDIA DIGITS」という、学習したいデータセットやモデルの選択など、必要な操作を全てブラウザ上で行えるツールだ。このツールは本来ダウンロードして実行するものなのだが、今回はNVIDIAのオンライン学習サイト「QwikLabs」の無料コースからクラウド（AWS）上に環境が整えられた仮想OSを使用する。そのため、DIGITSのダウンロードの必要もないし、PCにハイスペックなGPUが載っている必要もない。

　本記事で解説する内容はQwikLabsにサインインすれば誰でも体験できるため、やってみたい方はQwikLabsに無料登録、サインインしてみてほしい。

ディープラーニングに必要な操作がWebブラウザ上で完結するNVIDIA DIGITS

今回はQwikLabsの無料コースで体験する

ディープラーニングって？

　先に、ディープラーニングの基本的な概念を見ていこう。ディープラーニング（≒ディープニューラルネットワーク）は、機械学習の一種である人工ニューラルネットワークの中でも層が多層になっているものを指す。ディープラーニングの図というと下のような図を見たことがある人もいるだろう。

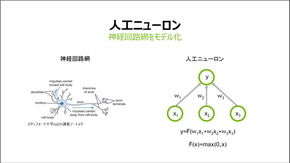
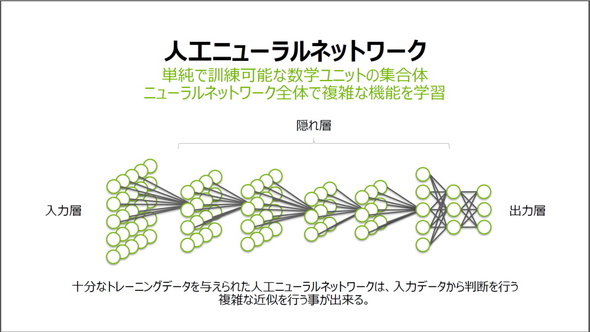ディープラーニングの説明でよくある図。入力層に画像や音声などのデータを入力し、出力層でそれが何であるか判別する（スライドはNVIDIA Deep Learning Institute 2017の村上真奈氏と森野慎也氏の講座から引用）

　この図の丸は生物の神経細胞（ニューロン）を模しており、丸どうしをつなぐ線は神経細胞どうしをつなぐ神経線維に対応する。つまり、人工ニューラルネットワークとは生物の神経回路をまねることで機械でもデータを学習しようというアプローチだ。

人工ニューロンの正体

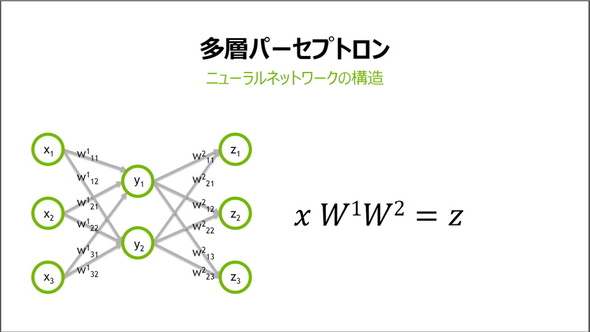
　では、神経細胞に当たるこの「丸」は具体的に何なのかという疑問が浮かぶ。神経細胞をまねるというから何かしらのオブジェクトだったり、データセットだったりするのだろうかと前はふんわり思っていたのだが、説明を聞いてみると答えは明快。単なる変数だ。

人工ニューラルネットワークは生物の神経回路をまねたもの（左）、神経細胞に当たる「丸」の正体は単なる変数（右）

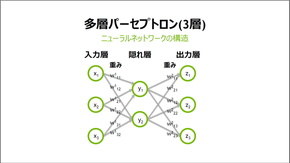
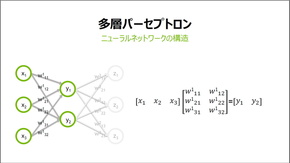
　入力層の各xにそれぞれ「重み」の係数wをかけたものを隠れ層の各yに加算し、各yにまた重み係数をかけたものを出力層zに加算する、という操作を表したものが上記右側の3層のパーセプトロンだ。例えば入力データに白黒画像を使うなら、入力層のxの値は各ピクセルの明度になる。

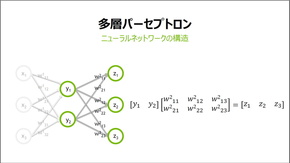
　つまり、このパーセプトロンは数字の乗算と加算しかやっておらず（他の関数操作が加わる場合もある）、小学生でも理解できる計算式で表せるのだ。この図には入力層、出力層の変数が3つしかないので3つの方程式で表せるが、実際には3つよりもっと多いため、行列を用いることですっきり表せる。

入力層から隠れ層、隠れ層から出力層への計算は行列で表せる

行列計算をまとめると入力層から出力層への計算は1つの式で表せる

重みの調整が人工ニューラルネットワークの要

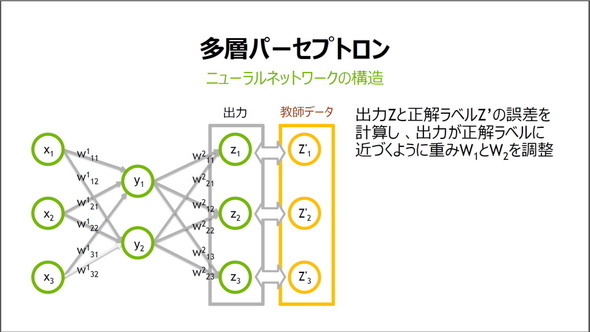
　重みwは初めはランダムに生成されるため、出力層の値は教師データ（正解の値）と比べると当然めちゃくちゃだ。教師データとの誤差が小さくなるよう、ここから重みwの値を勾配降下法などのアルゴリズムを使って調整していく。

出てきた出力層の結果と正解の値を照らし合わせ、差が小さくなるように重みを調整していく

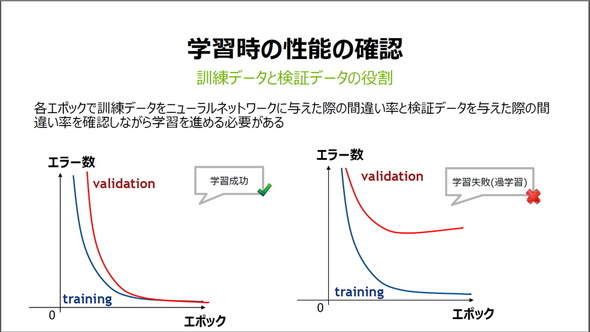
　ディープラーニングの学習では、使用するデータを訓練データと検証データに分ける必要がある。訓練データで学習（重みの調整）し、検証データで学習がうまくいったか確認する、という具合だ。検証データはエラー数を確認するだけで、あくまで重みの調整には使用しない。訓練データの学習から検証データでの確認までの一巡を「エポック」と呼び、基本的にエポックを増やすほどエラー数が小さくなる（＝正答率が上がる）。

なぜ検証データを分けるのか→未知のデータに答えられなくなるのを防ぐため

　なぜ検証データを分けるかというと、「過学習」という状態を避けるためだ。過学習は訓練データに対してはよく正答できるが、その他の未知のデータに対してはうまく答えられない状態のこと。従って、エポックを繰り返しても検証データでエラー数が下がらなければ過学習、つまり学習失敗であり、逆に検証データでもエラー数が下がれば学習成功ということだ。

「過学習」を避けるため、収集したデータは訓練用と検証用に分ける必要がある。検証データでもエラー数が下がっていけば学習成功